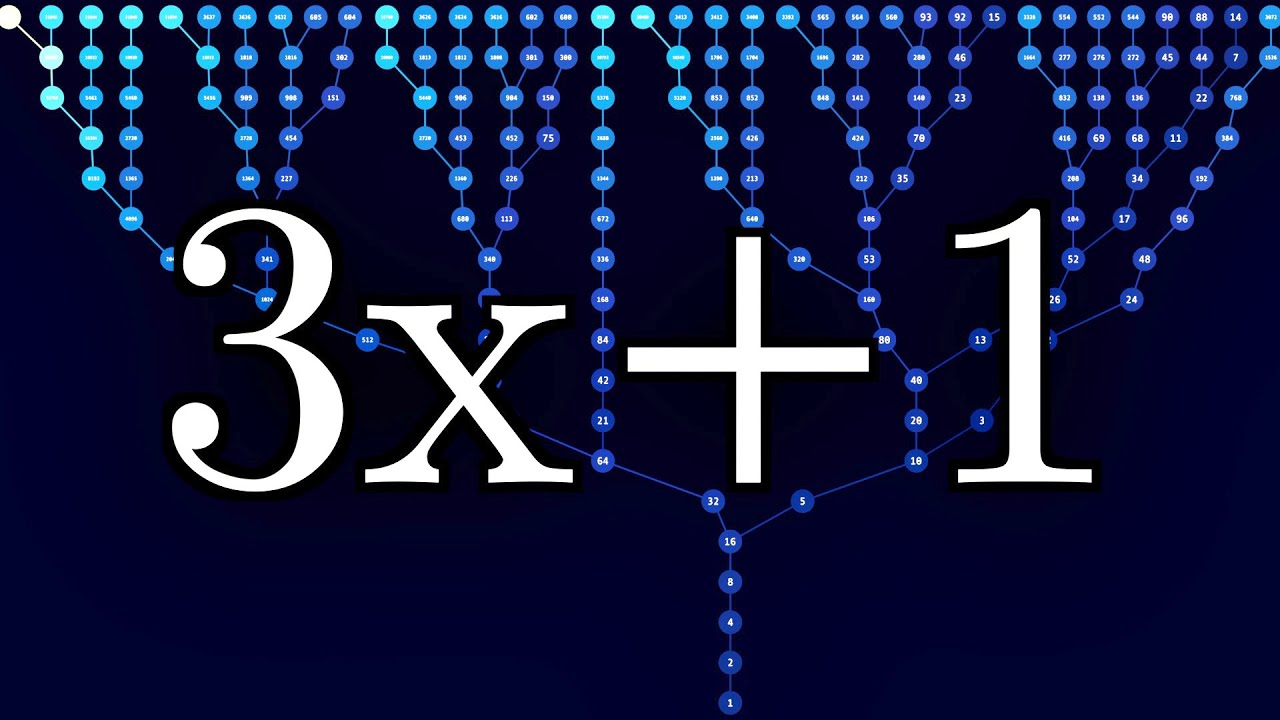Not a jee related problem but...
https://www.youtube.com/watch?v=094y1Z2wpJg
I don't exactly understand what the problem is? Also, these were some other thoughts I had:
1. If we apply the 3x+1 step the number always increases and becomes even. On dividing by 2 the number may be odd or even.
2. If one number doesn't satisfy condition, by multiplying by 2, infinitely many numbers don't satisfy the condition. Further, the list of numbers must end in some closed cycle. Further if we assume the highest term as a and the term before that b, so that 3b+1=a (b is odd, a is even.). Now all other terms must be of form a/2^n (including b). (The highest term must be even and lowest term must be odd as 3x+1 increases and x/2 decreases the number)
3. Now, 2^(n)b=a=3b+1. So b=1/(2^n-1), whose only solution is 1. So if a sequence of numbers ends in a closed cycle, the cycle must be {1 2
2 4
4 1}?
1}?
I don't exactly understand what the problem is? Also, these were some other thoughts I had:
1. If we apply the 3x+1 step the number always increases and becomes even. On dividing by 2 the number may be odd or even.
2. If one number doesn't satisfy condition, by multiplying by 2, infinitely many numbers don't satisfy the condition. Further, the list of numbers must end in some closed cycle. Further if we assume the highest term as a and the term before that b, so that 3b+1=a (b is odd, a is even.). Now all other terms must be of form a/2^n (including b). (The highest term must be even and lowest term must be odd as 3x+1 increases and x/2 decreases the number)
3. Now, 2^(n)b=a=3b+1. So b=1/(2^n-1), whose only solution is 1. So if a sequence of numbers ends in a closed cycle, the cycle must be {1
 2
2 4
4 1}?
1}?YouTubeVeritasium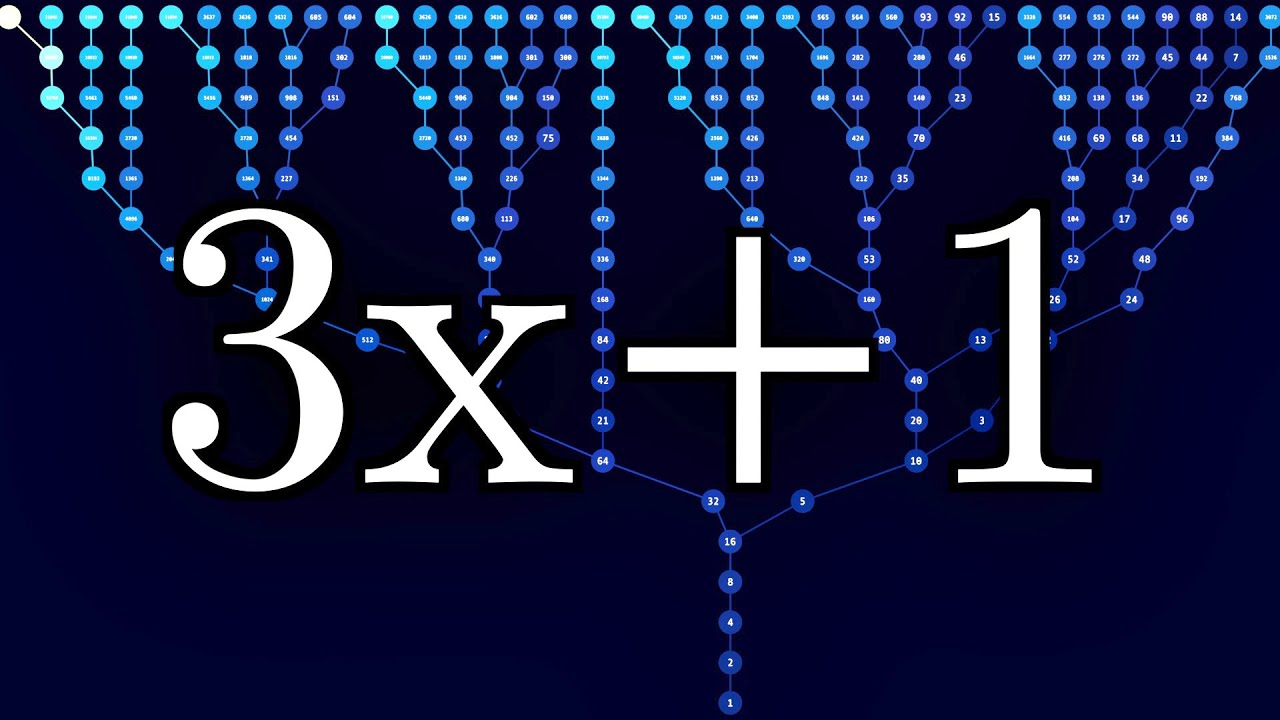
The Collatz Conjecture is the simplest math problem no one can solve — it is easy enough for almost anyone to understand but notoriously difficult to solve. This video is sponsored by Brilliant. The first 200 people to sign up via https://brilliant.org/veritasium get 20% off a yearly subscription.
Special thanks to Prof. Alex Kontorovich for in...
Special thanks to Prof. Alex Kontorovich for in...