✅ Optimizing number matching algorithm for a logical game
Hey, I'm trying to optimize one function from my solver thats is the most performance critical area.
The idea is that I have a grid x by y of numbers 1-9 (0 is an empty cell).
Numbers must be next to each other horizontally, vertically, or diagonally. There can't be any number between them. Distance between the cells has no limit. Find all valid pairs.
I have 2 approaches
1.https://pastecode.io/s/11vo1bcs
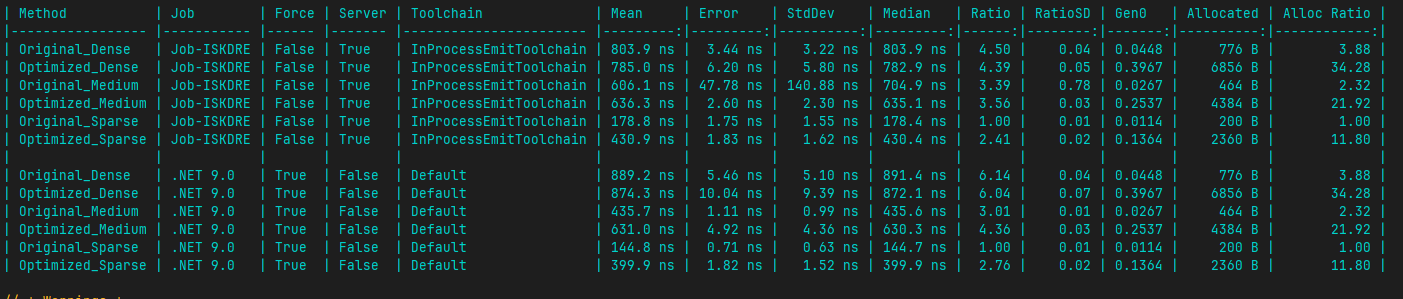
I've attached image showing the results.
Thanks in advance!
The idea is that I have a grid x by y of numbers 1-9 (0 is an empty cell).
Numbers must be next to each other horizontally, vertically, or diagonally. There can't be any number between them. Distance between the cells has no limit. Find all valid pairs.
I have 2 approaches
1.https://pastecode.io/s/11vo1bcs
- this approach first pre-processes the grid to find and store the locations of every number. After this phase, it iterates thru each number's stored positions and checks every possible pair to see if they can be connected. A separate function verifies if the path between two positions is valid.
- https://pastecode.io/s/gmp701ig checks every cell in the grid. For each cell containing a number, it does a linear search in specific directions (right, down, and two diagonals) to find a matching number. The search stops if a match is found or if the path is blocked by a non-zero number
I've attached image showing the results.
Original_ stands for the first approach and Optimized_ for the second one. Looks like my optimized approach isn't really faster which kinda makes no sense for me cuz it should make less checks, but anyway. Which approach should I choose? Are there better ways to do that? What low level optimizations can I do? I'm trying to push this as far as I can. Thanks in advance!