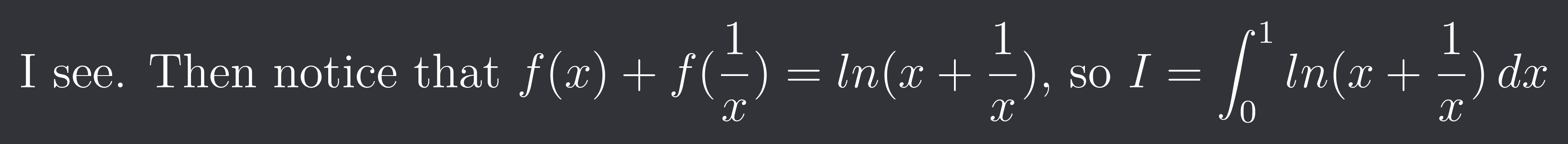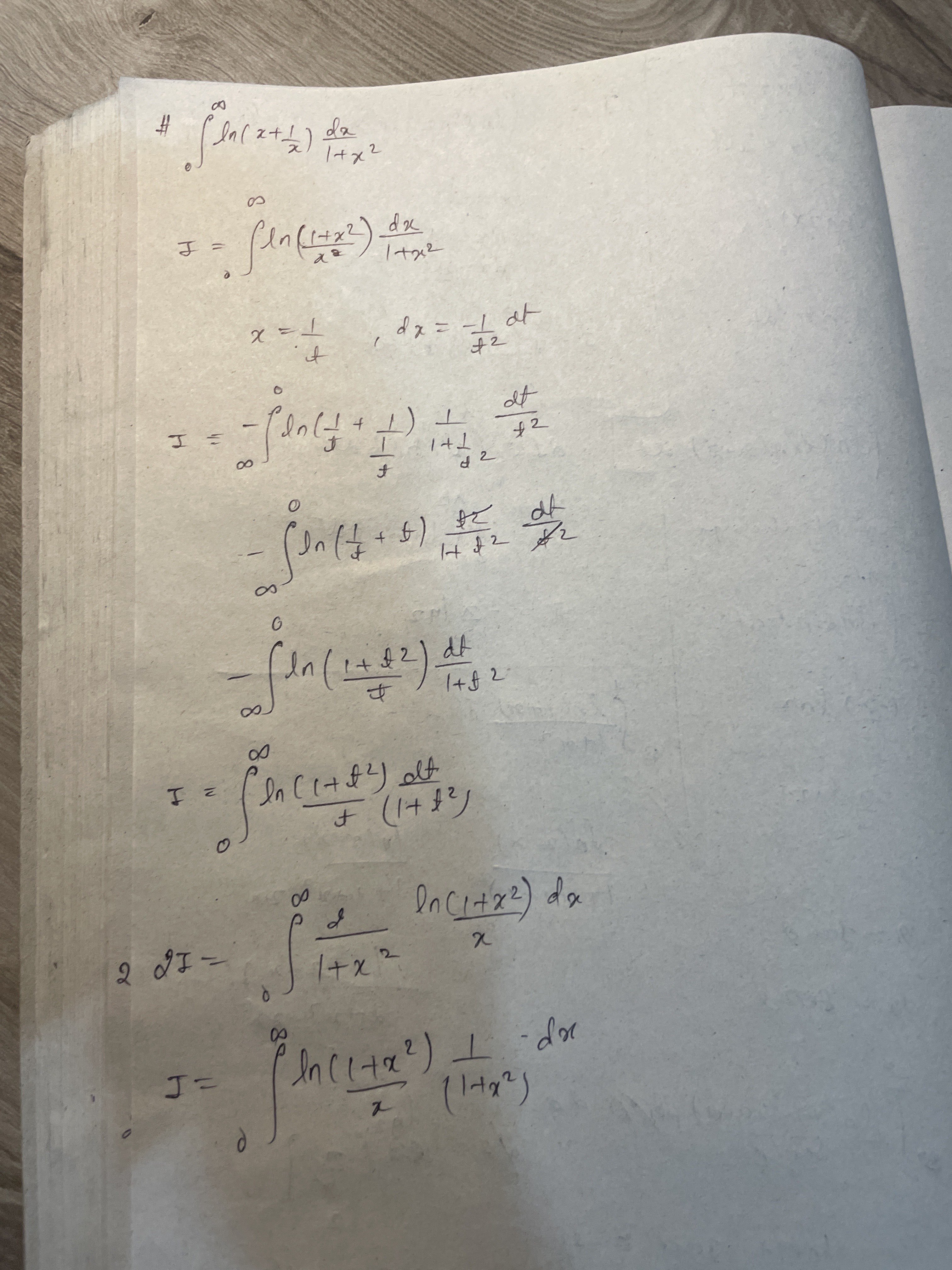definite integral
Im using reciprocal property here but idk where im doing wring the ans is piLn2
17 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.did u reverse the sign twice?
Umm...
Why not substitute x=tan(theta)
That will do the trick ig.
Oh my bad
But even after that how come we’ll get ln2?
Oh yeah that would definitely work but im currently focused on learning this reciprocal thing
I see. Then notice that $f(x)+f(\frac{1}{x})=ln(x+\frac{1}{x})$, so $I=\int_{0}^{1} ln(x+\frac{1}{x}) ,dx$
SirLancelotDuLac
Also you seem to have changed sign twice in 5th line of solving (one while intechanging limits and other inside the log.)
After correction im getting this
,rotate
Yep. This is correct, but the reciprocal thing becomes the question itself.
Apart from tan(theta) sub., the other way is this ig.
Ah it seems to me that the tan(thetha) thing would work better here
intense!
sorted?
Yup
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@1088352651567173632> (1088352651567173632)
Time
<t:1727514367:R>
Solved by
<@1075951732460376214> (1075951732460376214)