52 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.?
ghost ping
Yeah, I took components wrong
oh
can u explain how do I start
,rotate
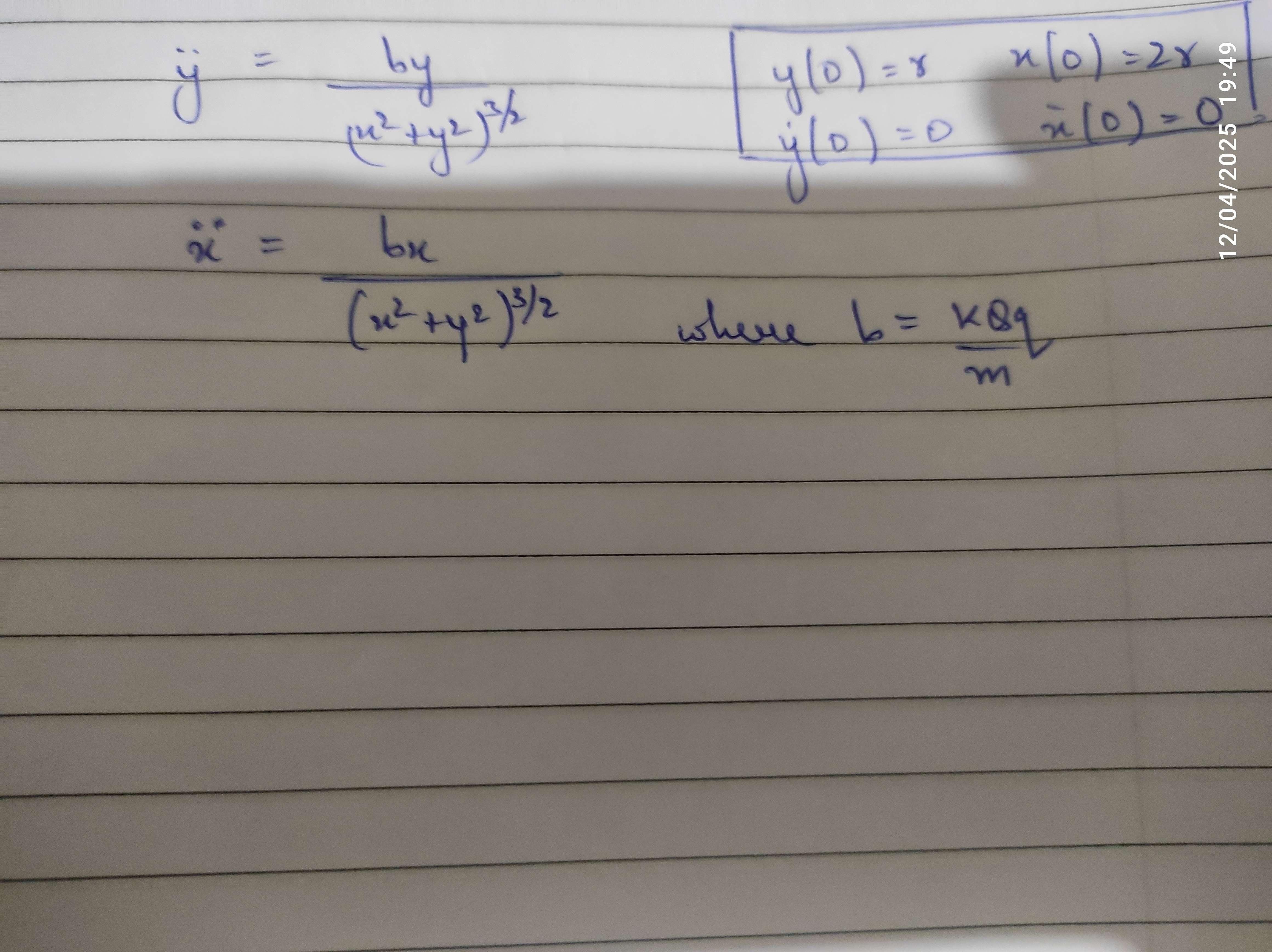
x is position of Q, y is position of q
I started off here
hmm
I got this differential eqn
but I dont know what to do after that
does it require some subsitition
That's what I'm thinking
Ok, yeah, square both equations and add them
Take x²+y² = r²
what does that do
Just a sec, I'm checking if it works
alright
Damn no, it doesn't help
sad
what if we try centre of mass?
Oh wait it does work
oh
Ok, so, consider the point (x,y) right?
ok
Now, it's an imaginary point such that its x component is the position of Q, and y component is position of q.
These equations of motion we got apply to it
yup
But by squaring both and adding, we get a single dimensional equation in acceleration and it's position
yes
And once it's a single dimension motions, we can solve right?
wait a single dimentional
ok yes
yes ong
ok so I got this
a = b/r^2
@Opt
arent we deriving what we would get using energy conservation?
whats a
No, it's a=b/r²
But there is an issue. We can't take components.
@SirLancelotDuLac I think you should take a look
what
why
we assume r to be a vecot
(x,y) = (r, theta)
Yes, but our equation here is strictly for the absolute value (length)
Ok, that's not how it works, just saying.
it works, we're getting what we sould get from energy
@Opt
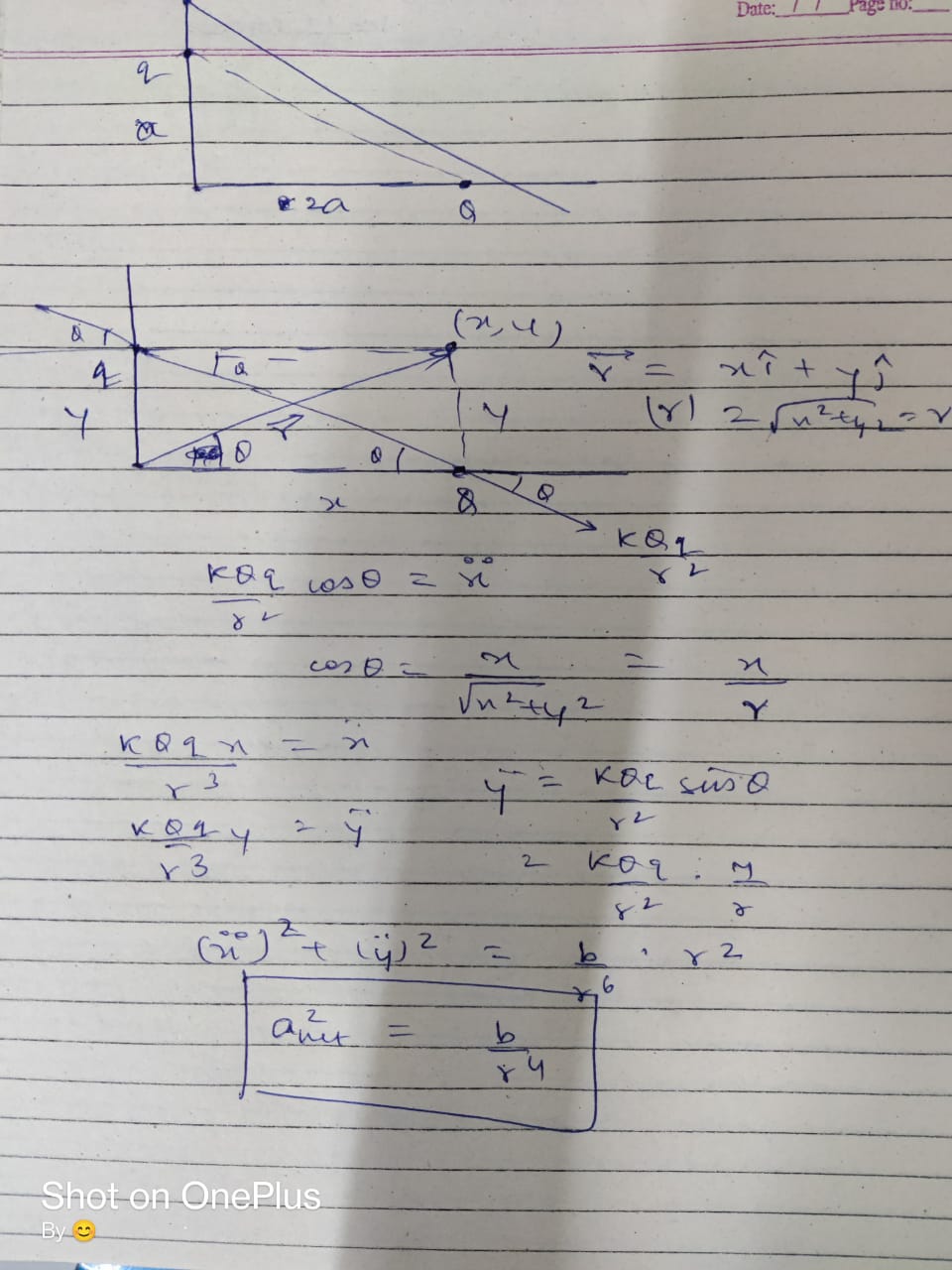
Well, yeah, but how are you gonna know the angle?
The angle is changing too
y does acceleration not depend on angle
if we've solved everything correctly then accn doesnt depend on the angle
nahi toh somthing is wrong
The scalar value of these does not depend on angle
As vectors....
hmm
so whats the exact way to get a relation between accn and r,theta
Hmm...I'm just getting a very long second order DE.
why not use com
Normal force acts in the x and y-directions on q and Q respectively.
yes
but we can still use com
How so?
idk but I feel we can
There is external force, and finding out the normal might be equally challenging as finding the kinematics of the particles.
Oh, wait, I think the angle theta remains conserved.
same
but idk how do I prove that
cuz using that we can easily say that com moves in a straight line
Oh that makes it easy then.
Yep, ig this gives 4r as the required distance.
yes
amazing
the book's soln is this @Opt @SirLancelotDuLac

I really overthought this didn't i?
idk but
the a = b/r^2 relation was correct @Opt
cuz when you solve it you get work energy theorem
Ah yes. Angle hence remains conserved.
+solved @SirLancelotDuLac @Opt
Post locked and archived successfully!
Archived by
<@831415988636614696> (831415988636614696)
Time
<t:1744732827:R>
Solved by
<@1075951732460376214> (1075951732460376214), <@763645886500175892> (763645886500175892)
