Rotation, polygon rolling

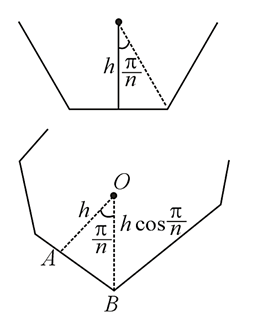
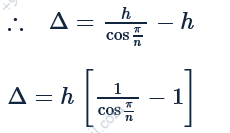Consider regular polygons with number of sides n=3,4,5… as shown in the figure. The center of mass of all the polygons is at height h from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the center of mass for each polygon is Δ . Then, Δ depends on n and h as