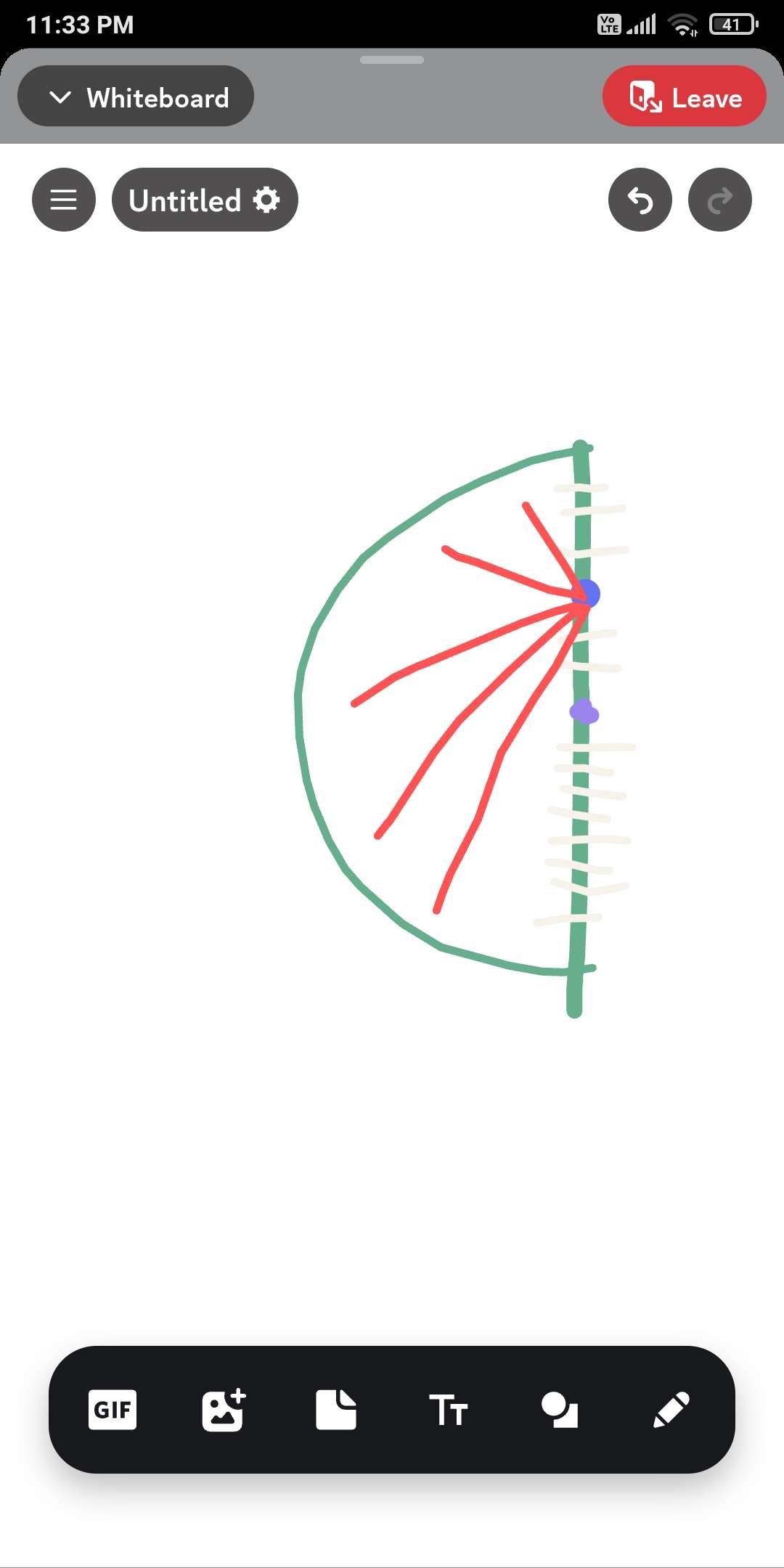
Electrostat
To ye semicircular ring h uniform charge density ki and mujhe jo blue pint h uske about nikalni h field. Lets say ki blue point ka altitude given
To fir iske upar field kese nikalenge. I thought of integrating the e vectors depicted in red but distance is also changing .
Could also look at it like a bended rod
To fir iske upar field kese nikalenge. I thought of integrating the e vectors depicted in red but distance is also changing .
Could also look at it like a bended rod