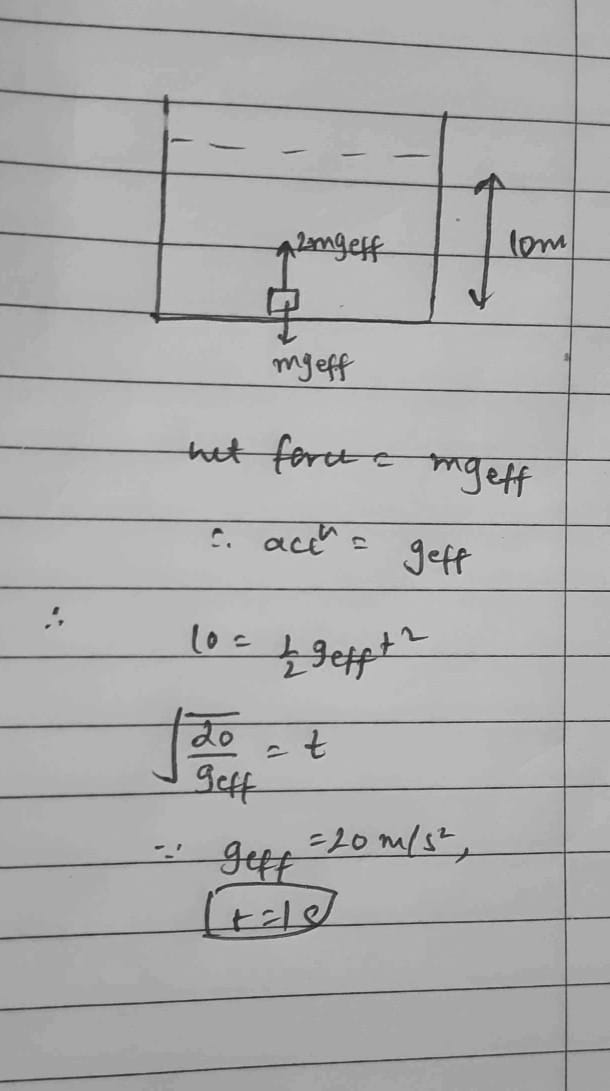
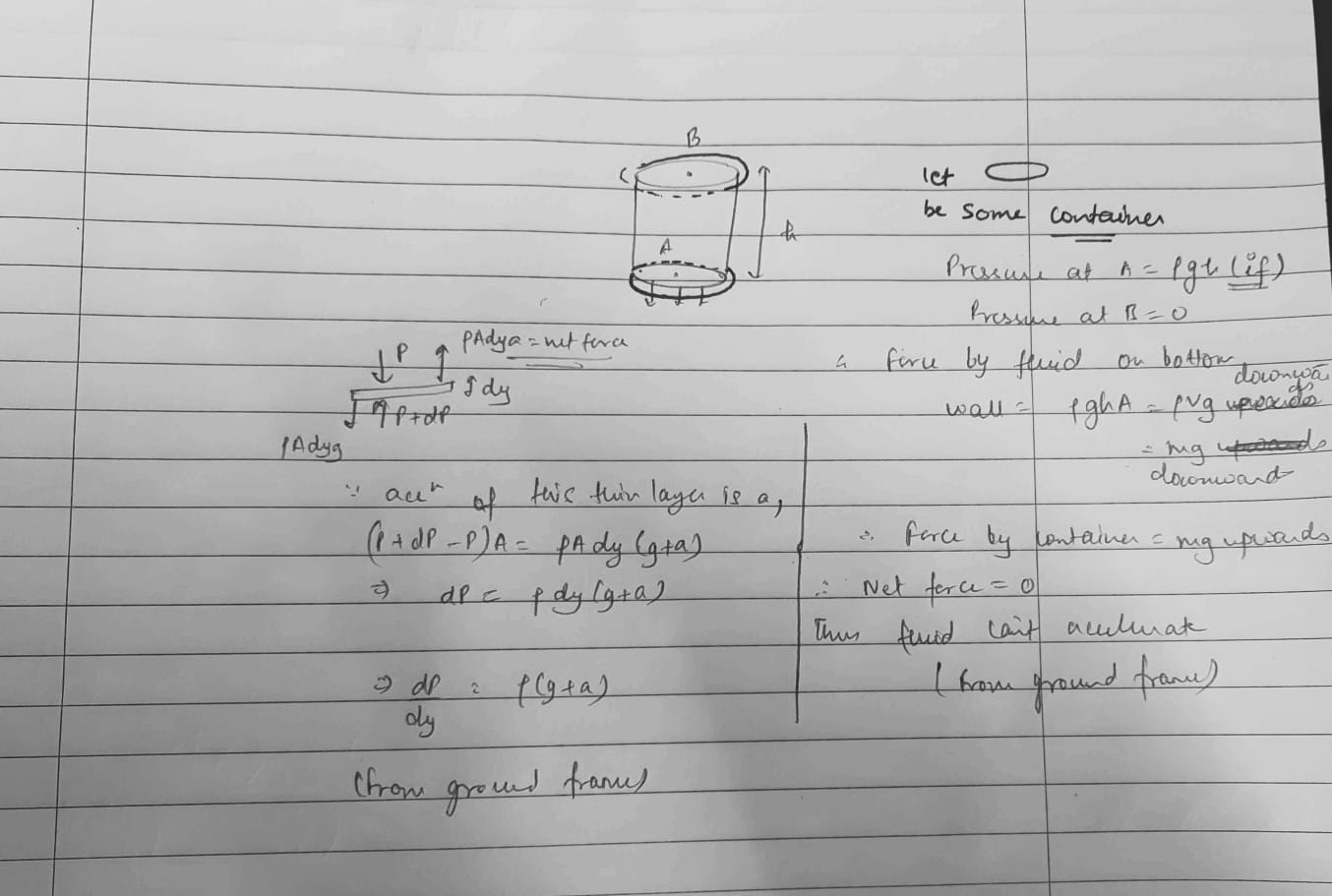
Fluids + NLM
wont net force on this be 0? psudeo force + mg = Boyouncy Force
so shouldnt ans be D? since it will inf time
40 Replies
@Gyro Gearloose
Note for OP
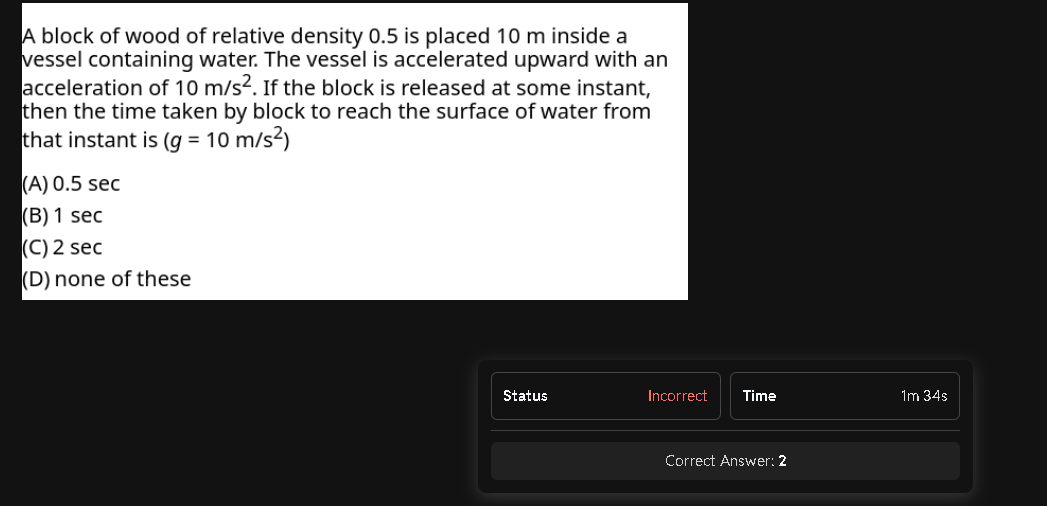
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Initial position mein mg=Buoyancy, but when container is accelerated and block is released from the original position, there is an imbalance of pseudo force.
This imbalance pushes the block upwards.
it said it accelrated first , then at some instant block is released
Yes. The block is kept at its initial position (by some unspecified force) and then released, whence the imbalance pushes the block.
what imbalance
The one due to pseudo-force.
Or rather the increased buoyant force due to increase in g_effective.
bro assume mg = F/2 , ma is also F/2 , Boyuoncyy force = F , all cancel out
when taking psudeo force why would g effective change?
*Rather than taking pseudo-force if you want to do by g_effective in that case
ah ic
still
it will balance
idk why it will move
(Via the g_eff approach)
Initially it is kept at 10m depth by unspecified forces.
but what about the case where we take psuedo force , why is force 0 there , we get inf time , what is wrong in that approach
i think the q is saying that the block accelerates with 10, this isnt the same 10 that cancels g, theres 20 units of acceleration upwards
no it def says the vessel is acc , not the block
fair enough, i didnt note that
Vessel is accelerating upwards right? Now the pseudo-force on the block is downward, but there is also pseudo-force (downward) on the liquid, so the liquid exerts more buoyant force on the block. (Because now pressure gradient is higher with depth). So, the forces do not cancel out.
OOOH
wait , psudeo force is downward on liquid , so it will become more dense , and because of more dense bouoynt force will increase thats why forces dont cancel , but how much denser will it become? cant say anything about that
A rather correct way than saying "more dense" (since fluid is incompressible) would be the pressure gradient increases. As for by how much does it increase, consider a thin layer of width dy, then pressure dP on it would be rho.A.dy.(g+a)/A, so dP/dy=rho.(g+a) (where a is acceleration of the vessel)
ok and how will that pressure gradient affect force?
Bouyancy is due to pressure difference, so it does affect buoyancy which affect the force on the object.
isnt it Vrhog
Consider a cylinder. The pressure upwards on the bottom face is P(d+h)*A while that at the top is P(d).A (where P(x) is pressure at depth x, d is depth of top face and h, A are height and area of cylinder). So buoyant force is [P(d+h)-P(h)]A.
If the pressure is rho.g.h, then it becomes rho.g.h.A=rho.V.g
Since here the pressure is 2rho.g.h (which you can see from here), the bouyancy is 2rho.V.g
well , due to psudeo force pressure will increase ye , but the diffrence in pressure will still remain same no?
No, the rate at which pressure increases increases. So pressure difference will indeed increase.
i dont quite understand this
Well buoyancy is due to pressure difference at two points right? Now the pseudo-force increases the pressure exerted by each thin layer of fluid; so pressure increases more quickly as compared to the normal condition here. So pressure difference between 2 points with same vertical distance is more in this case as compared to the normal condition, hence buoyancy (which is due to pressure difference) increases in this case. This increased buoyancy is the answer to what you did not take into account here.
Well my counter argument is that lets take a point A it has lets say 0 pressure due to liquid i took base here , and pusedo force
now point B at height H , it has pressure Rho G and puseodo force
the psudeo force is same in both , so the pressure diffrence remains constant
Okay, Imagine a cylinder of height h from B to A. If you say the pressure at bottom is rho.g.h times higher than at B, the fluid experiences a force of rho.g.h.A in upwards direction (from ground frame, that is). This is balanced by the force of gravity so the cylinder should not have any motion in ground frame.
The correct thing would be the pressure difference is rho.h.(g+a). (Which is in line with the g_effective wali approach)
uid experiences a force of rho.g.h.A in upwards direction (from ground frame, that is). This is balanced by the force of gravity so the cylinder should not have any motion in ground frame. , i dont understand this part
i still dont understand where there would be a pressure diffrence at all
psudeo force will remain constant throught the liquid
This is from the ground frame. (The image) If we take inertial frame, then the explanation would be similar. (Pseudo-force in downward direction+weight of liquid) is balanced by extra pressure exerted on the fluid by the bottom layer.
where u get this from?
Force by the bottom layer is (P+dP)A while that by the top layer is PA
So just force balancing, dP.A-mg=ma and since m=rho.A.dy for a thin layer of dy thickness, dP.A=rho.A.dy(g+a)
ah ic
ye mathematically i can see the result , but in the physical sense i still dont get it , like the pusedo force is Constant it will just get canceled out when taking change
No. Each layer is to be to be in equillibrium right? Due to pseudo-force each layer experiences an extra downward force. To balance this out, the bottom layer would have to put more pressure; so the difference in pressure with height (Keyword being difference) increases.
Like, if the extra pressure on the first layer is p, the second one gets an extra pressure of p downwards, so the third layer exerts 2p extra pressure on the second one, the fourth one, 3p extra pressure on the 3rd one and so on.
(Assuming each layer have an extra pressure p to keep it in equilibrium from pseudo-force apart from weight)
ye man idk why , i just dont feel it on a intuitiave level
Ah. Will try to think of a nice example.
i still think that force is constant it should cancel
@Gamertug The only example I could think of was this adjacent question:
Consider planks arranged in a stack and numbered 1,2...n from top to bottom. Then, let plank 2 exert a force N1 on plank 1, plank 3 exert N2 on plank 2 and so on. What is the value of Nk, if the system is accelerating with acceleration=a upwards? (Where k<=(n-1)). Now let the value of n tend to infinity, and planks be infinitesimally thin. Then what is the value of (N(x+dx)-N(x))/dm where dm is the mass of this infinitesimally small plank and N(x+dx) and N(x) are normal forces exerted by the next and previous plank respectively (and here, x is distance of plank from top). And final question, what do the previous answers tell you about the rate of increase of pressure with a and x?