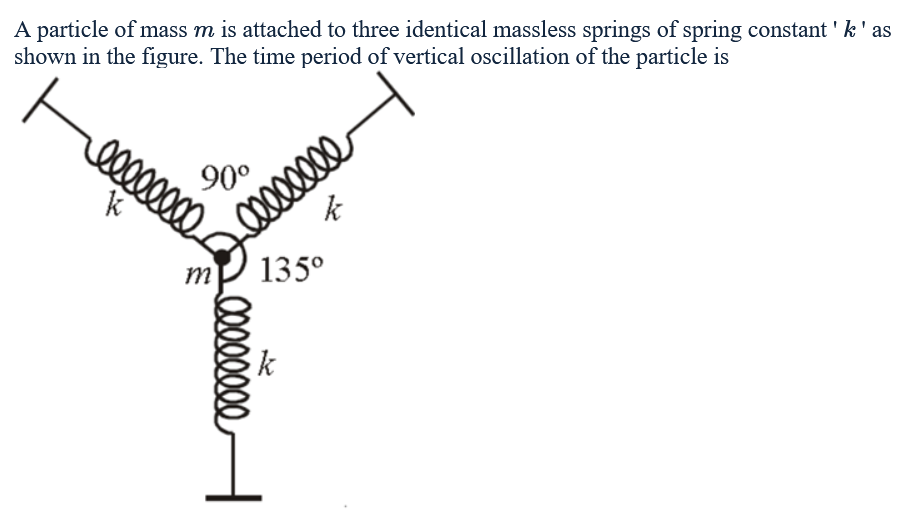
SHM, time period of spring system
I guess I'm having trouble in the geometry? Not sure. How do we find K_equivalent?
Ans is 2pi * sqrt(m/2K)
11 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Displace slightly the mass downwards by a distance x, so the extension in the upper strings is x/sqrt(2), i.e., they exert a force of kx/sqrt(2) on the particle, which add up to kx/2*2 by the upper springs. kx by the lower spring makes the net force F=-2kx, so time period would be 2pisqrt(m/2k)
ah ok
why is the displacement on the upper strings x/sqrt(2)?
i'm having trouble with the geometry of that
Consider a small change in height of oobject as x downwards, then change in length of string is $\sqrt{\frac{l^{2}}{2}+(\frac{l}{\sqrt{2}}+x)^{2}}-l$
Okay, yeah I got the text right. :sweaty:
SirLancelotDuLac
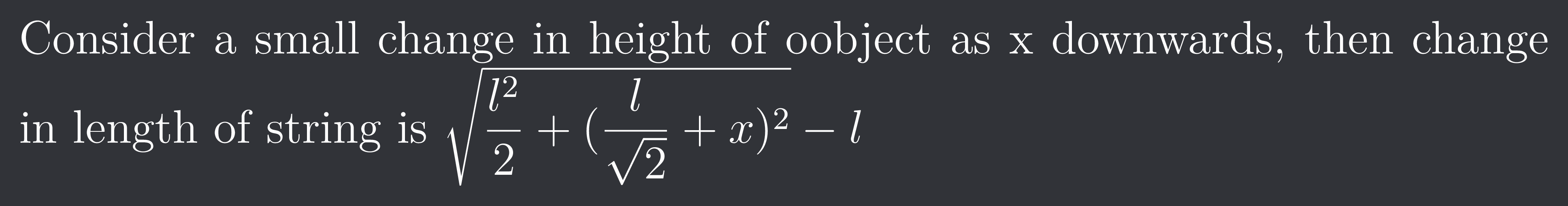
Neglecting x^2 and above order terms, inside the square root we get l^2+sqrt(2)lx and then doing binomial approximation we would get x/sqrt(2) as the value of extension.
wow okay
lemme try to prove that
Or instead of doing all that you could see that the string are perpendicular to each other, so let elongation in each one be y, then vector sum of y would be x or 2cos(45)y=x or y=x/sqrt(2).
Bruh, why did I reach binomial approximation and stuff 🤦♂️
i didn't generalize it to this extent but i got the change in length
x*cos(45) tryna do this lmao
50th time's the charm yes
lmaoo real
overthinking this is probably why i didnt get it
yeah this makes a lot more sense
that was what was in my intuition but i didnt know how to frame it
thanku 🫡
+solved SirLancelotDuLacPost locked and archived successfully!
Archived by
<@759051317124792351> (759051317124792351)
Time
<t:1745411424:R>
Solved by
<@1075951732460376214> (1075951732460376214)