24 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.How I could've thought of this is completely beyond me
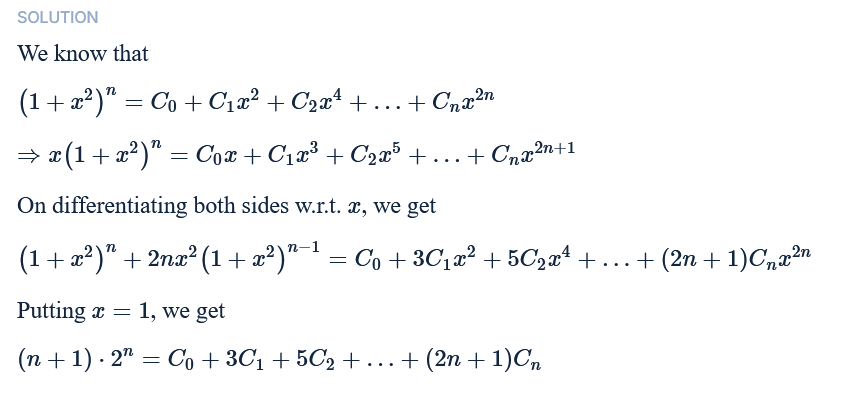
Idk if I'm missing a topic or something but that solution does not seem intuitive
It's not intuitive don't worry
It just comes from practice
🧍
I tried something else
I created one 2^n using the C0 available
Okay I absolutely don't know why people do this in simpler cases :/
Then there's two C1 available, using which i can create 2*2^(n-1)
And then I keep adding and subtracting the C1 required to create 2^(n-1)
Until I get to
n
How do I complete that expression and generalize it idkYeah exactly.Write C_0+(2n+1)C_n as (n+1)(C_0+C_n) and keep writing other stuff like this too.
So you have (n+1)(C_0+C_1+...C_n)
Which is basically 2^n(n+1)
wait what
Huh. I wouldn't have thought of that ngl. The differentiation seems more intuitive to me.
wait how are they equal
C_0+(2n+1)C_n and (n+1)(C_0+C_n)
ah C0 = C_n = 1
oh
how th do u do these manipulations
yeah lmao that's an amazing manipulation
my brain lagged looking at that
lemme try to complete this
are there 2 middle terms or one middle term
there's 2 middle terms if
n is odd which folds nicely into the same manipulation
if n is even there's 1 middle term
what happens to that oneThen the coefficient will be (n+1)
Because n+1 will be the odd number
holy shit wow it is
beautiful
how on earth did you think of this
wow
amazing
Seen this question before, so I thought it then.
how did you think of it then bro 😭
i genuinely wanna know
raw, unconscious pattern matching?
if that's the case then i just needa practice more
It was more like in 11th, I was lazy to differentiate and stuff.
So, my go-to in binomial was to not use differentiation at all. (If possible)
raw determination LMAO
is my method the same thing
i'm unsure how to actually complete my method to an arbitrary
nYeah, if you had followed similar trains of thoughts you would have stumbled on the same.
also does this differentiation method have a name or a search tag which i can look up to see more questions of this type
it feels different, in your method you're using the
C_r = C_(n-r) equality
actually ill give my method more thought and then decideYeah man ig your method works something like this:
Initially make 2^n from 1 of each term
Then 2(2^n-C_0) from 2 of all remaining terms
Then 2(2^n-C_0-C_1) from 2 of further remaining terms and so on,
You then get 2^n+(2^(n+1)+2^(n+1)+...n times)-(2nC_0+(2n-1)C_1+....)
Simplify the last bracket in last line to 2n(C_0+C_1+...)-(1.C_1+2C_2+....)
The results of both are known.
Ig this works. *(I seem to have messed up calculations a lot but yeah...)
best way i can think of is-
sum of (2r+1)nCr r = 0 to n
u mustve studied sum(r * nCr) = n2^n-1 and sum(nCr)= 2^n
simply put the values