LMVT
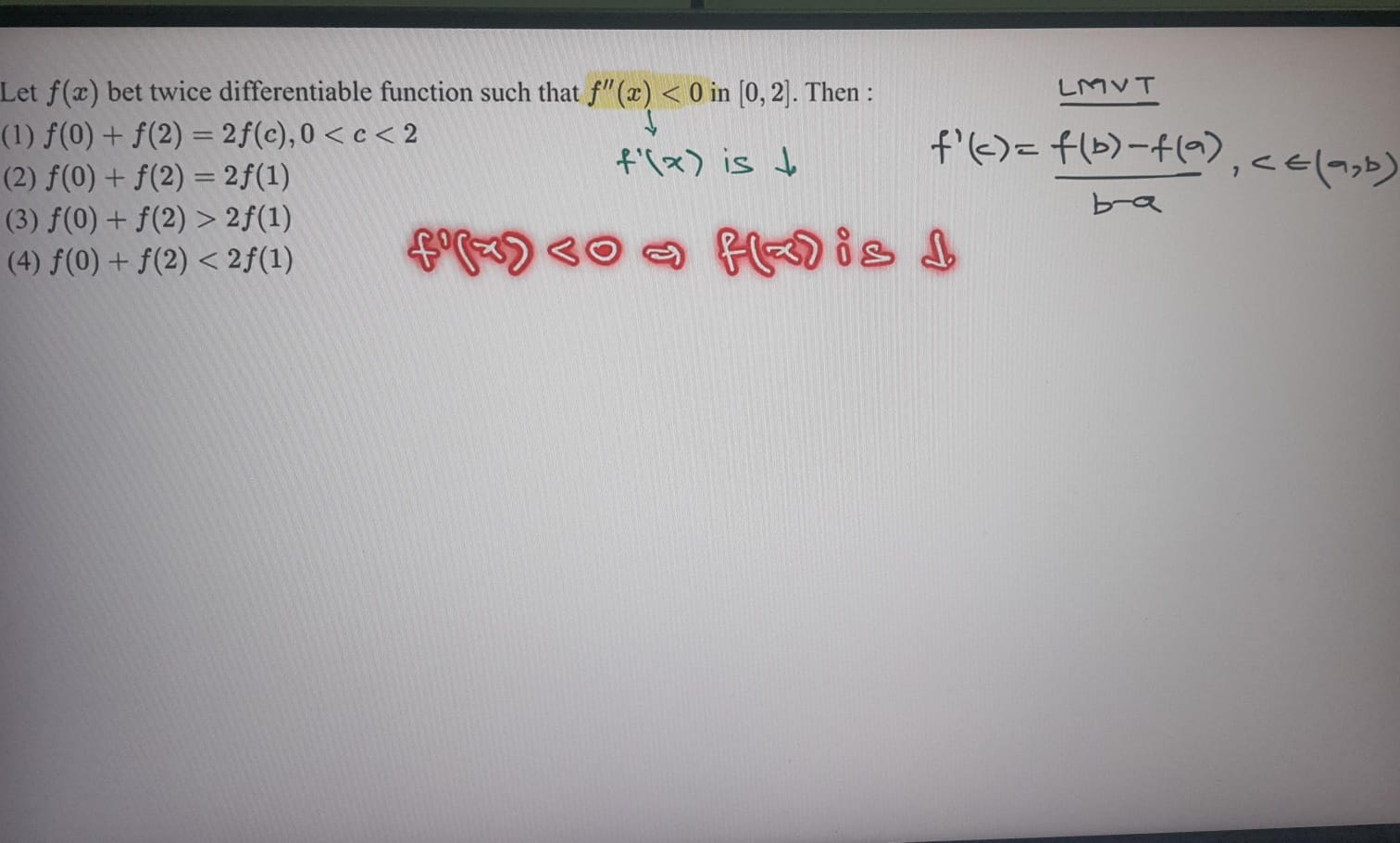
In the solution of the question, it is written that since f''(x) <0, f'(x) < 0 and f(x) is decreasing function which is not true right? f'(x)>0 AND f''(x) < 0 is also possible ig? So is there another method for solving this question?


13 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.The condition you mention is possible. Consider the function -(e^x)
All of it's derivatives are always negative (except as x→-∞ but we don't care about that)
For the first one shouldn't the interval be [0,2] and not (0,2)
Example, consider -x(x-2), f(0)+f(2)=0=2f(2)=2f(0)
Here c=0 or c=2.
I know that the condition is possible but since they haven't given any information regarding the function, whatever properties we use should be valid for all functions right?
yesss
f''<0 means the function is concave down. Now joining f(0) and f(2), by definition, there must exist a c in [0,2] (which is apparent after drawing a rough sketch) such that f(0)+f(2)=2f(c)
got it
but how do you prove this
In a similar manner. By concavity the midpoint of the line joining (0,f(0)) and (2,f(2)) (which is (1,(f(0)+f(2))/2) ) is below the graph which at x=1 acquires value f(1)
I don't get it
Can you show an illustration of this
please try plotting this on desmos/wolfram

