function
got y = -b^3 so [b] + [-b^3] + 4 is what we need to maximise but how do we do that?
15 Replies
@Apu
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.I got 3 somehow
how did u maximise the thing
AM-GM for r+(1/r)
oh i took a ar ar^2
so 1 = a (1+r+r^2)
b = a(ar) + (ar)(ar2) + a(ar2)
b = a2 (r + r2 + r3)
or b = r a^2 (1+r+r^2)
and y = a(ar)(ar^2)
y = -a^3 r^3 = -(ar)^3
b = ar
so y = -b^3
so expression is [b] + [-b^3] + 4
b > 0
so max should be 4
how do you get this using a ar ar^2
I am not sure
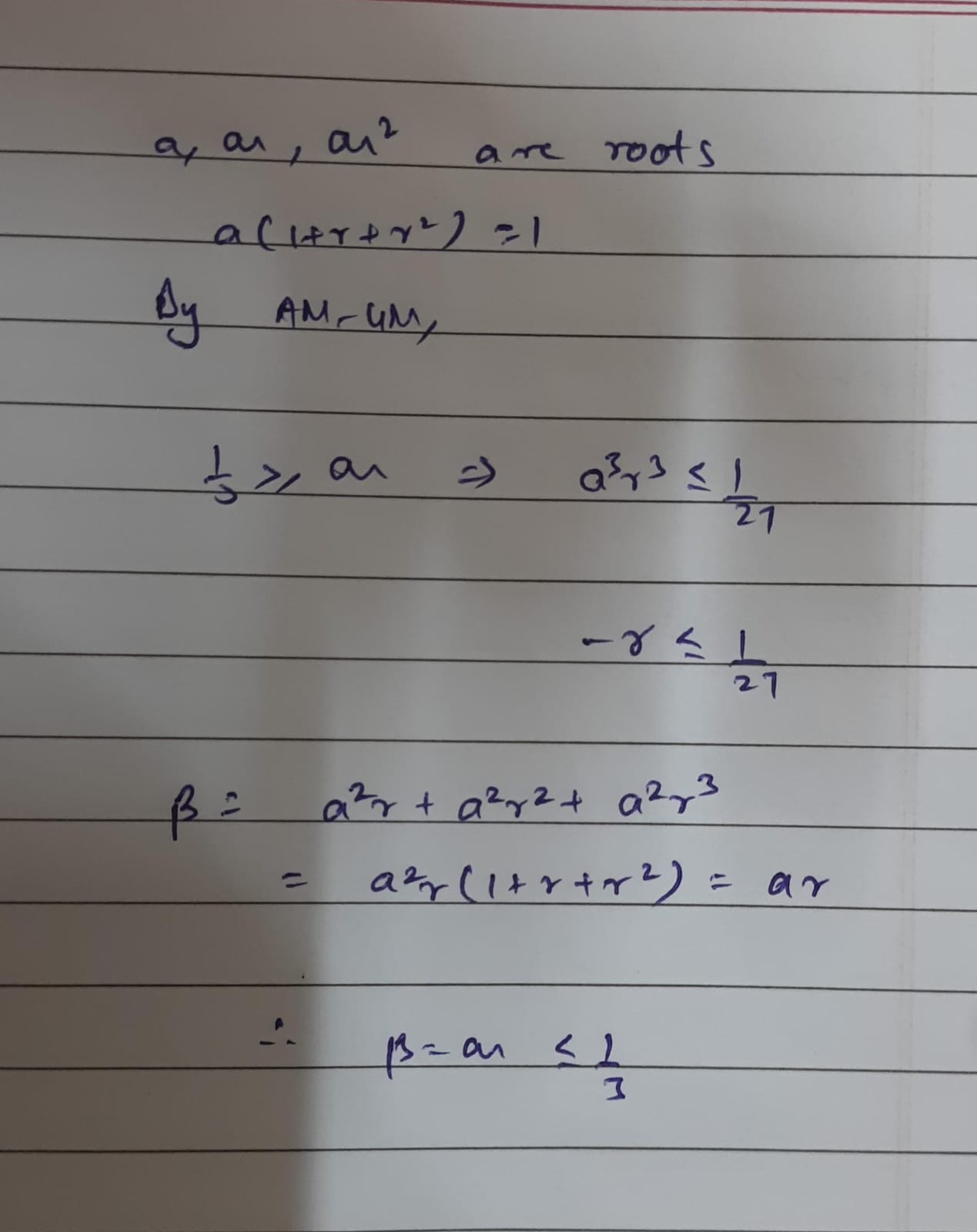
We have to maximize [b]+[-b^3], and we know that b=ar>0
So, from above [b]=0 and -1<-b^3<0
So the required value would be 0+(-1)+4=3.
Is the answer 3?
I got the same
I don't get what they mean by maximize tho, it would be a fixed value with the given constraints, right?
Yeah
beta lies in 0,1/3
+solved @Opt @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@1035556259417571408> (1035556259417571408)
Time
<t:1748145113:R>
Solved by
<@763645886500175892> (763645886500175892), <@1075951732460376214> (1075951732460376214)