35 Replies
Hello @Monishrules!
Choose the Study Helper subject ping
Choose the subject for the respective doubt :)
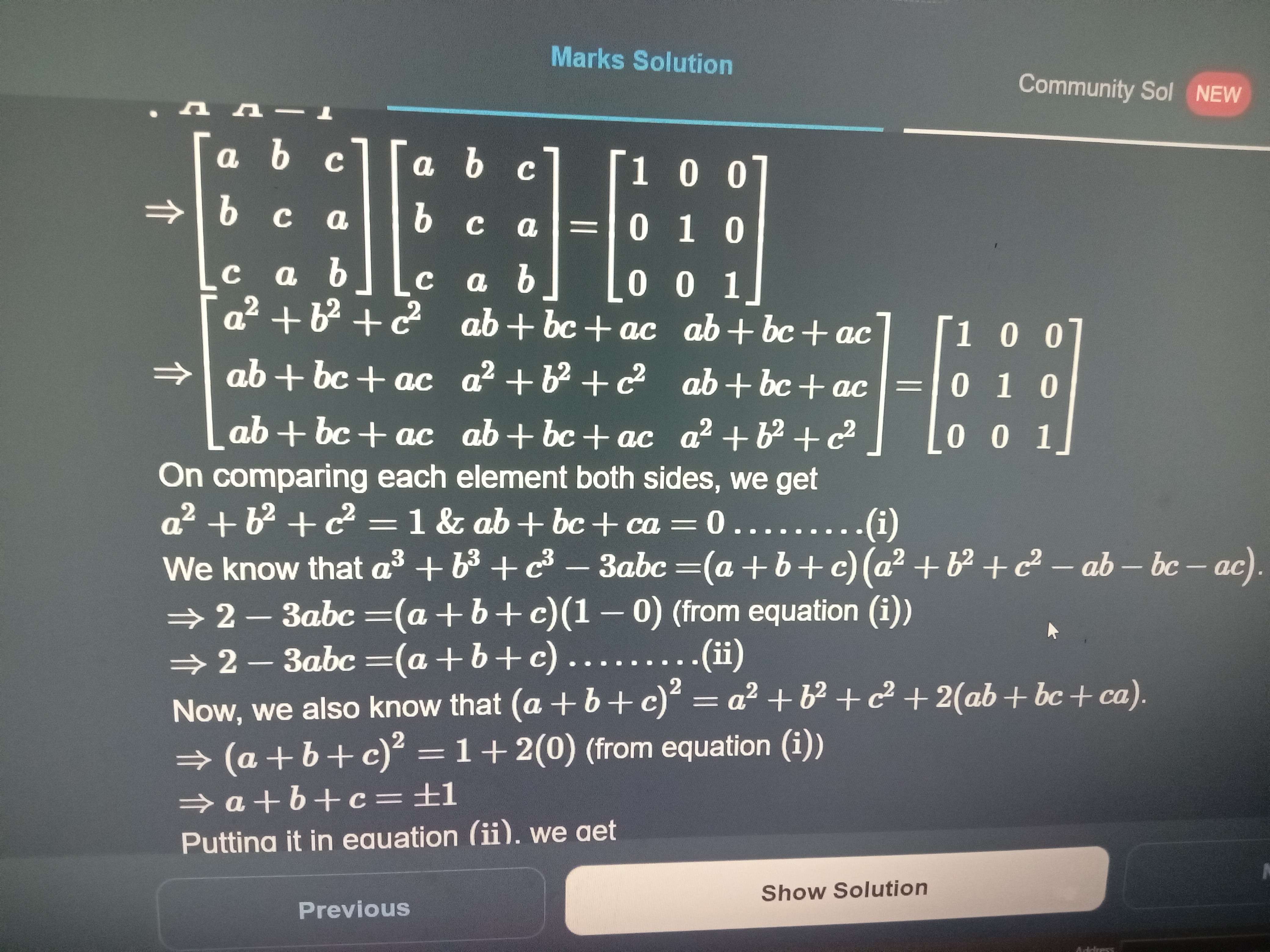
If A'A = I, then |A| = ±1
So 3abc-(a³+b³+c³)=±1
3abc = 2±1
abc = 3/3, 1/3 = 1,1/3
So the values are 1 and 1/3
Indiviual values for abc
Since a²+b²+c²=1
But a³+b³+c³=2???
Where did you get this from?
Orthogonal
Its a rotation matrix that means the basis vectors must have a magnitude of 1
It's not a rotation matrix though
Not all orthogonal matrices are rotation matrices
Ohhh
I didnt know that
Rotation matrix in 3D is weird.
I don't remember it
I thought all orthogonal matrices were rotational ones
So that holds in 2d but not in 3d
No? There are non-rotation orthogonal matrices in 2D too I'm pretty sure
Your method is a lot faster idk why they did all that but it does hold there
Hmm i do think all orthogonal matrices are rotational tho im like 99% sure
I had been using it in a lot of questions
If the det of a is +1 than its rotational according to wikj
So i guess i had been getting lucky xd
Det with -1 are reflections
Interesting
Gonna look into the proofs for tgat
Misconception aside the problem still stands that on regular multiplication we end up with sum of squares as 1
Ok yeah in 2d they have to be
Eh, don't do it like that
Just work it out, it's gonna be simpler
Det -1 means there's a reflection, but there could also be a rotation+reflection
I was about to ask this question in a different thread but but how can we be sure all orthogonal matrices in 3-D are not always rotational in nature?
Just a moment.
Nvm all orthogonal matrices have to be rotations
so det cannot be negative in 2 dimensions?
Because they're just a change of basis
now im confused 😕
Orthogonal matrices are matrices whose column vectors form an orthonormal basis of the space.
yes thats what i knew
So any orthogonal matrix would just be a matrix that changes the directions of coordinates you're working in, and since it's normalised, there's no scaling.
It's essentially a rotation of the axes
Man, I'm being dumb a lot of times today
but what about those with det -1 also that doesnt make sense because then it would a times a transpose = -I
ok
Those are not orthogonal by definition
That is the case where the right-handed coordinate becomes left-handed.
ahhhhhh
so they are still perpendicular
Orthonormal, yes.
Orthogonal and normalised
@
@Opt
so back to original q
Yes?
how is it possible
that a,b,c are real
Lemme see
Tbf it's a Mains question, so don't expect too much though
yeah i guess i was just bewildered
maybe im pissed because i didnt of the identity first
You good?