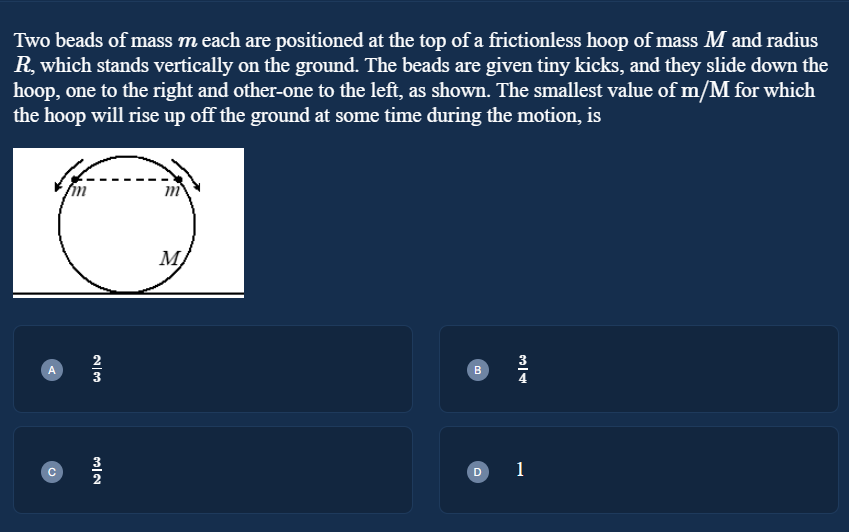
Two beads of mass m each are positioned at the top of a frictionless hoop
How to find the given value?
17 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Normal force has vertical component
it applies force up after the center is crossed?
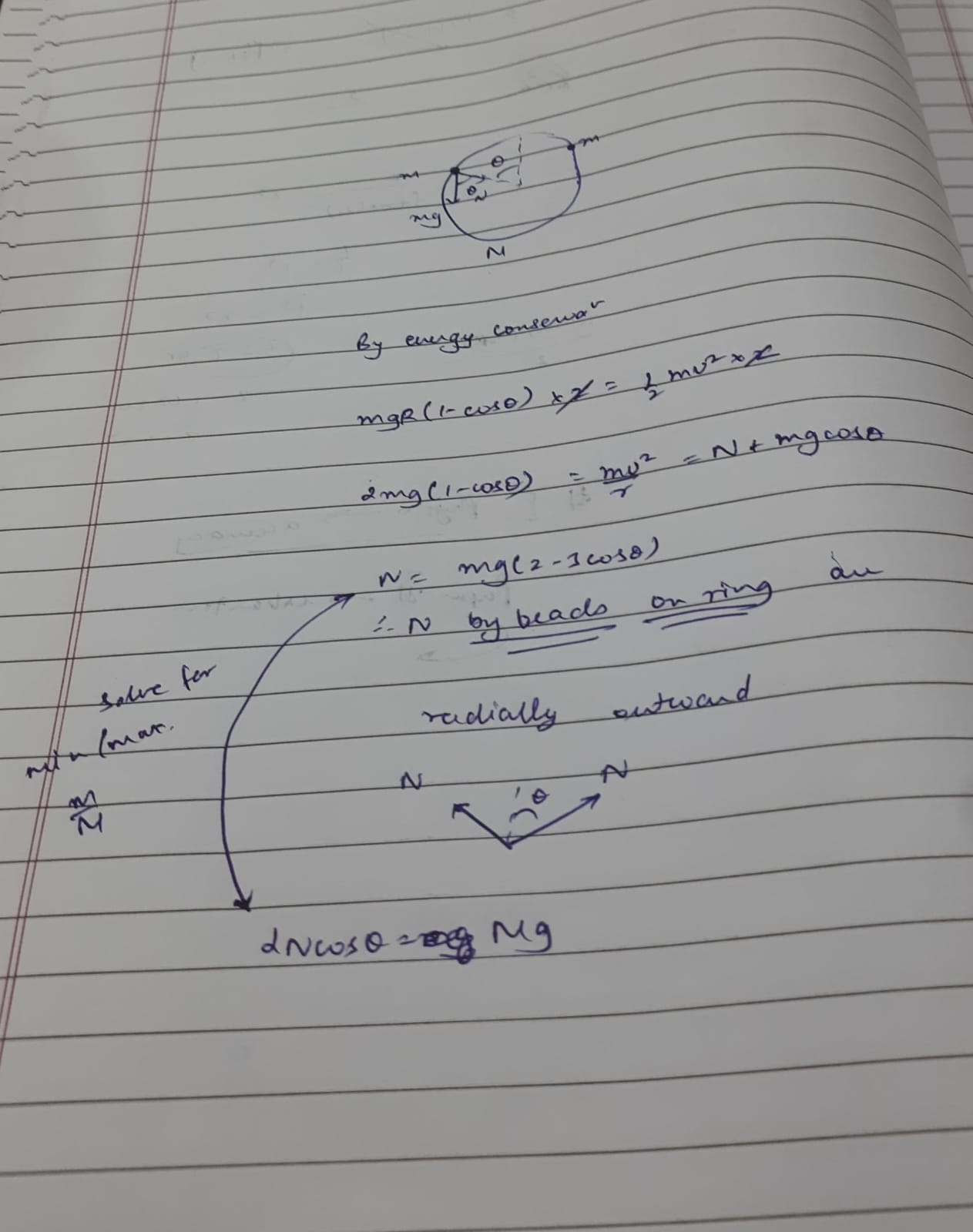
No, at all point. Ring applies a normal force outward equivalent to mv²/r, and that has a vertical component at all times
Apply energy conservation and find centripetal and hence normal, and use that to find vertical comp. of resultant.
wouldnt it apply downward force if above center
The normal is pushing the beads inwards, so by 3rd law, the beads push ring radially outward.
how inwards?
Something like this
The centripetal force of the beads is inwards correct? Thus, the tendency of normal by the ring would be to push the beads radially inwards.
Thus, the normal on ring by beads is opposite and radially outwards.
(When the mgcos(theta) component is not able to provide centripetal, as theta increases meaning this would decrease while the velocity and hence, centripetal increases.)
i thought the weight by beads would put a force on the ring and hence the ring would push it beads outward
But they are moving in a circular path right?
So there must be centripetal.
and what abt the weight by beads on the ring
Initially the mgcos(theta) component is too much and you are right, normal is outwards.
But velocity increases as beads come down and theta increases.
So mgcos(theta) is not able to provide appropriate centripetal
In which case the normal force steps in to provide the same, in radially inwards direction.
makes sense
Thank you so much
+solved @SirLancelotDuLac @Opt
Post locked and archived successfully!
Archived by
<@714440046429601792> (714440046429601792)
Time
<t:1747240815:R>
Solved by
<@1075951732460376214> (1075951732460376214), <@763645886500175892> (763645886500175892)