13 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.,rotate

Wait, why is degree 1?
There are 2 roots, precisely -1 and 0
After this, summation 1/f(r)=1/2(1/x-1/(x+2)); And hence this gets telescoped.

how do u get them
i understand how u related f^2(x) and f(x+1)
after that i need explanation
damn but howd you know to check at -2
The degree is the highest power of x in the expression. If the degree of f(x) is n, f^2(x) will have an order of 2n, since the highest power is the x-term gets squared. f(x+1) has the same order as f(x). By given constraints, we find 2n=n+2 or n=2. The expression is a bi-quadratic. We know that the 2 roots are 0 and -2. (From option B and plugging x=0). Now we plug in x=-1 to find f(x)=-1. Hence, the required quadratic is x(x+2).
The term $(x+2)\sqrt{1+(x+3)\sqrt{1+(x+4....)}}$ becomes zero 'cuz of the (x+2) term. So we have $-2\sqrt{1+(-2+1)}=0$
SirLancelotDuLac
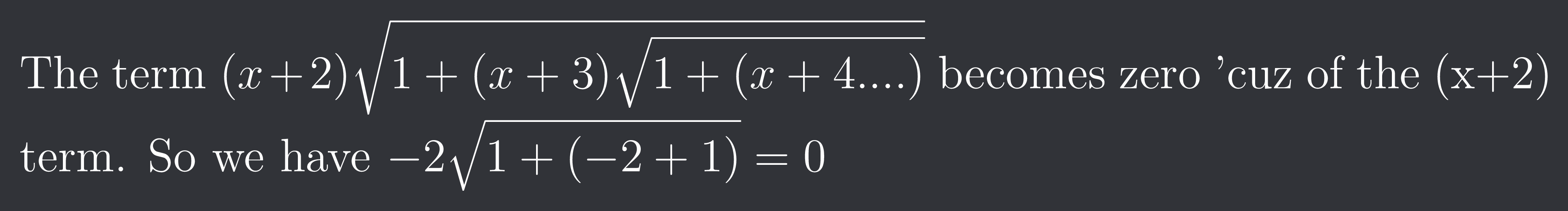
Yes but like if it was any higher degree or a diff polynomial wouldn't we need to check for -3,-4,etc
But here we know the degree is 2. (Refer to the solution above) and hence we stop after finding 2 roots.
Sorted?
