potential due to dipole
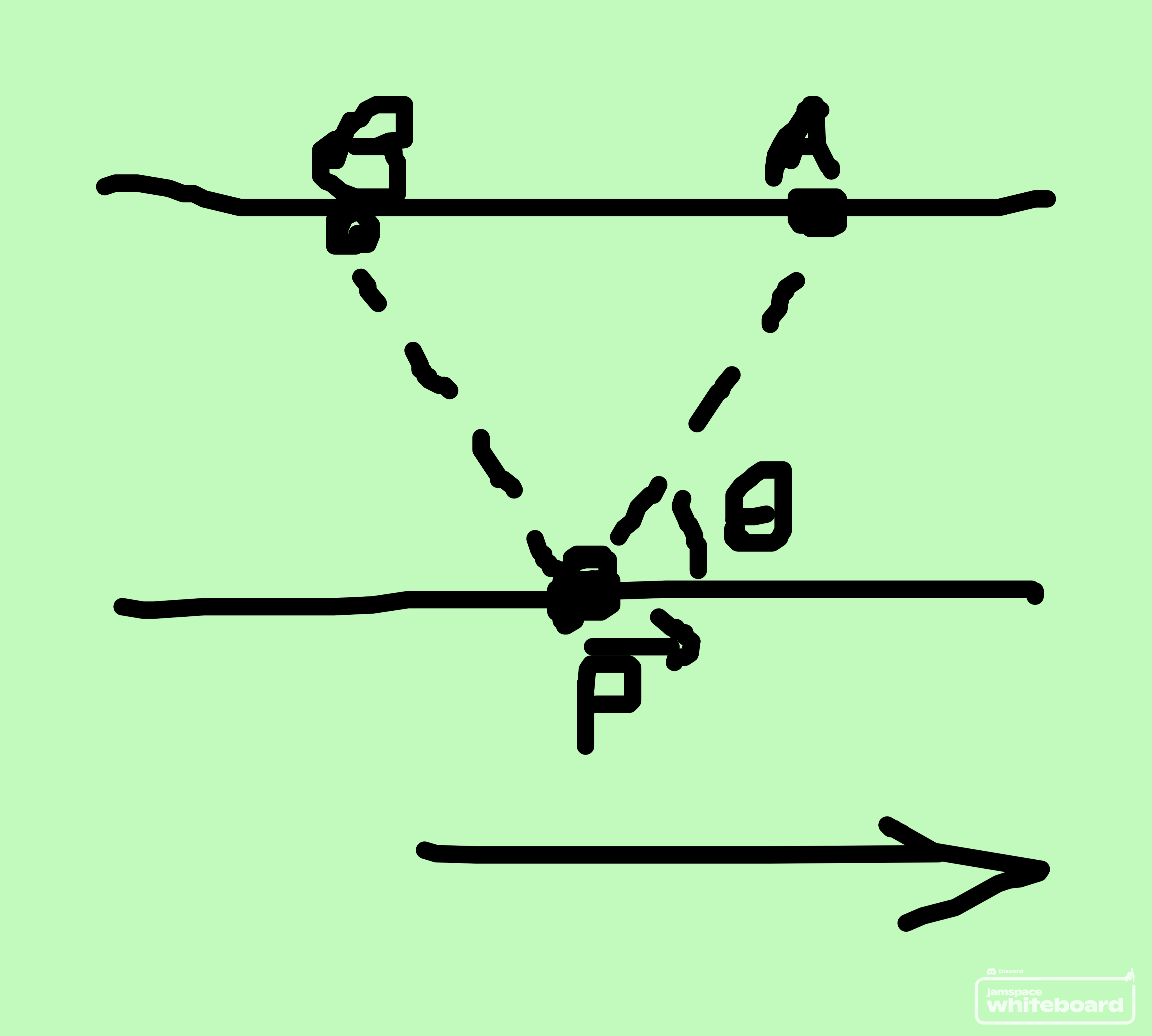
a charge q is moved from a to b in the region of a fixed dipole p. find the work done on the charge (assume gravity free space)
36 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.i am posting the diag in a min
V = Kp•r/r³
Given that dipole is at origin
thts wht i thought at first but the given ans is diff
Ok, give the diagram
Shared from Whiteboard
the ans given in book is
pqcos/2(pi)(epslon nod) r^2
What's q?
Also, there isn't sufficient information
In the diagram
q is the charge moved
from a to b
aakash modules 🤡
Send the original question na
this is the question this same diagram and the sentence i typed out
i dont have a phone rn to click picture
this
Ok, so, I'll assume that both points are a distance r, and by that logic, the angle on the other side is also theta
hn vo to tha mai banana bhul gyi 😅

,rotate

the given ans
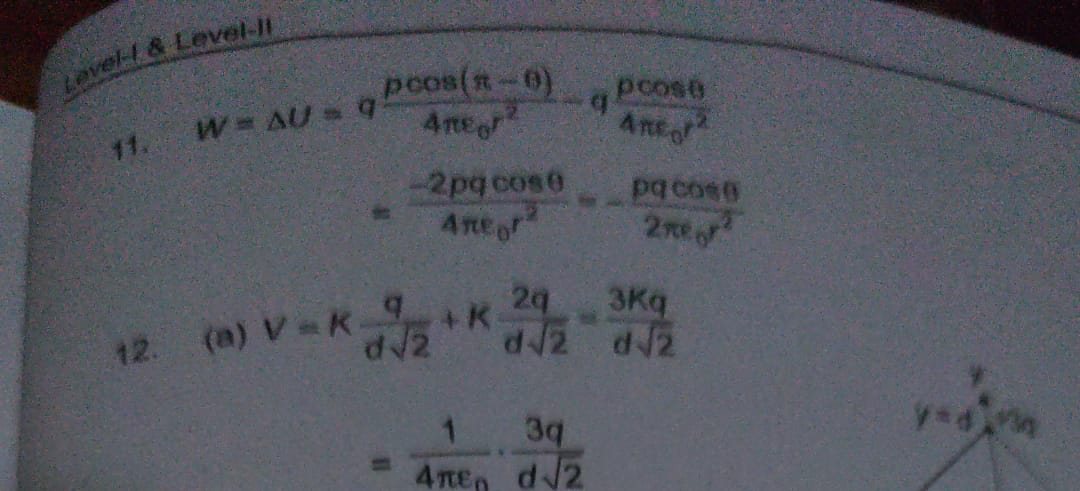
V(Q) = $Kp\hat{x}\cdot(r)(-cos\theta\hat{x}+sin\theta\hat{y})/r^{3}$
V(Q) = $-Kpcos(\theta)/r^{2}$
V(R) = $Kpcos(\theta)/r^{2}$
Yeah this is correct.
my question is how merko ye smaj nhi ara ki kaha se ara hai ye
the pi - theta
and all
Angle is taken with respect to positive direction of x axis
So clockwise it's theta. Anticlockwise it's π-theta
okk
but
Yeah
this says it is r cube
but the ans key says r square
Mb
R cancels up and down
First eqn is right
I forgot to cancel in second and third
Opt
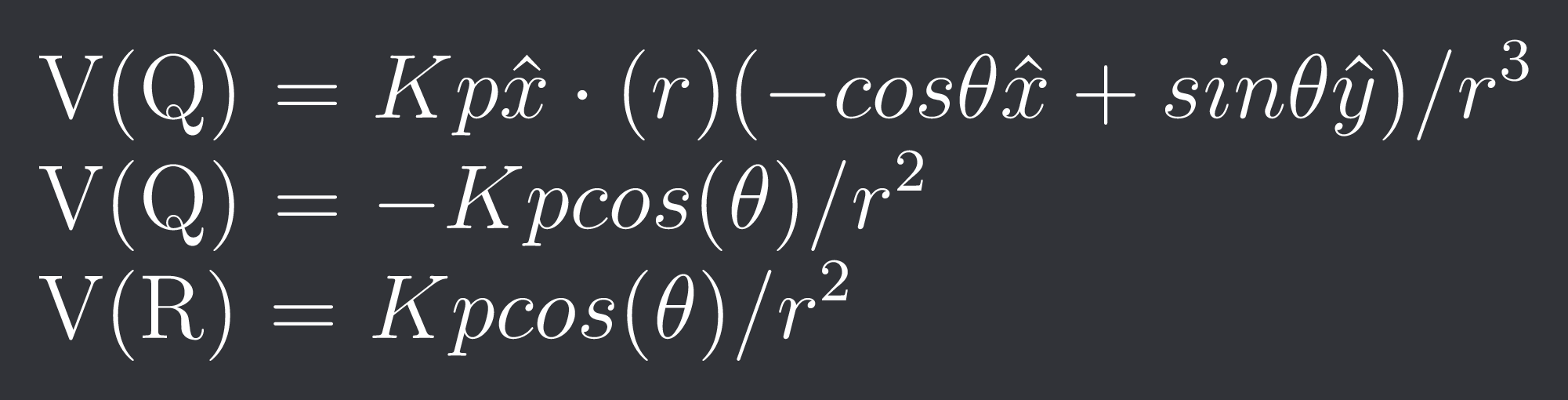
and ur one is kpcos
but here it if u convert it gives 2k right?
or am i doing another blunder?
? What? Convert what?
this is in expanded form of k right?
so when we turn it back to k
Yeah
It's going to be 2K, because you're doing V(R)-V(Q)
mujhe kuch bhi smaj nhi ara
i think i will try this once mre
phir bhi nhi aaya to dekhte puchti aapse
Ok
I'll head to sleep, it's laye
*late
yh sure
night
@Sephrina got it?
nopee i left it for a while will revisit
+solved @Opt
Post locked and archived successfully!
Archived by
<@888280831863451688> (888280831863451688)
Time
<t:1748719060:R>
Solved by
<@763645886500175892> (763645886500175892)