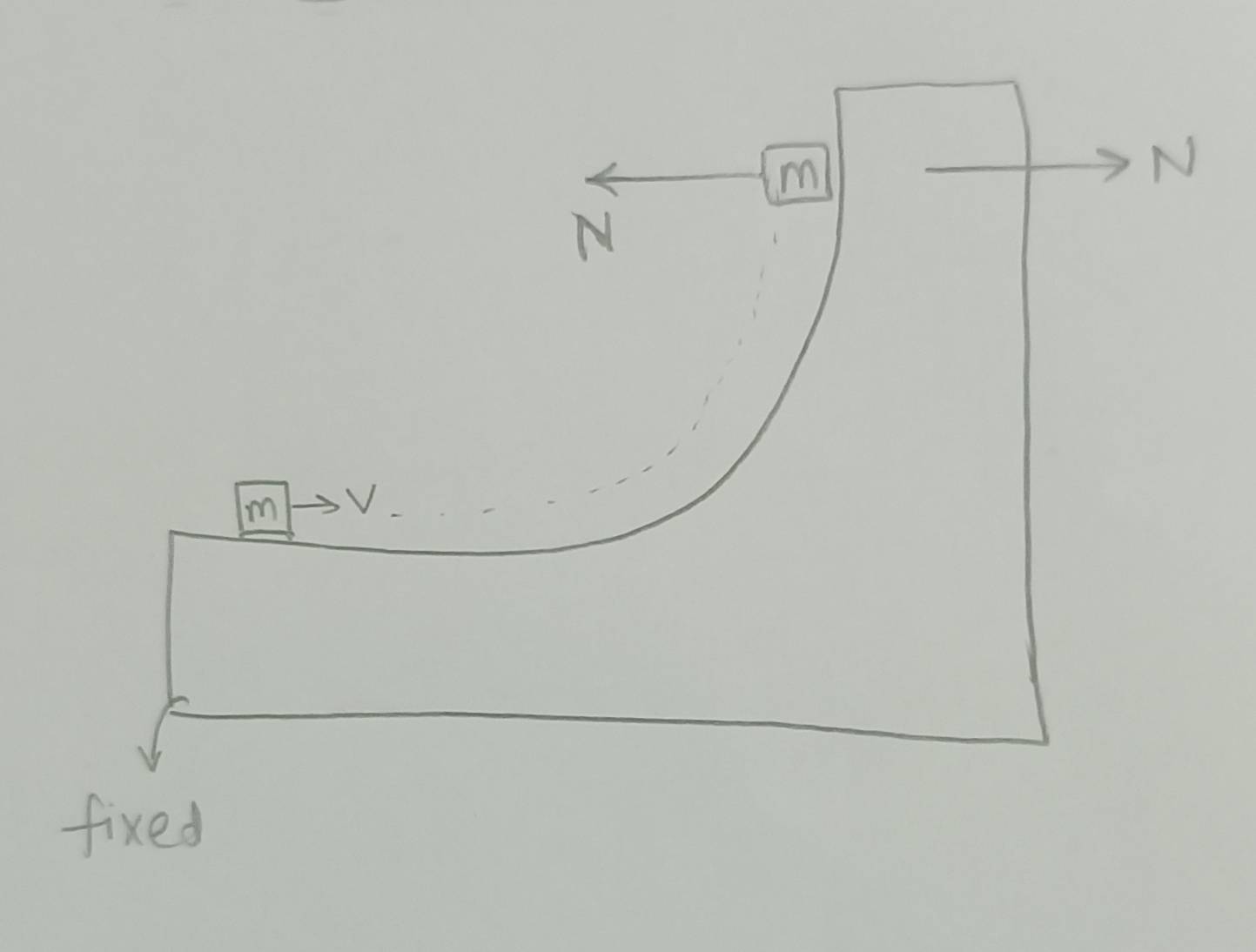
Momentum conservation

momentum consv means acceleration of centre of mass is zero, so i want to confirm it in this case...
at the top point when it comes to rest:

if we consider both wedge and block(we see the com of both of them), then both the normals cancel out and net force on com in x axis is zero so mom is consv in x axis.
if we only consider the block(we only see the com of the block), then there is nothing that balances the normal on the block(or it's com), hence can we say momentum is not conserved in x axis??

[ofcourse it's not consv in y axis that's clear to me]