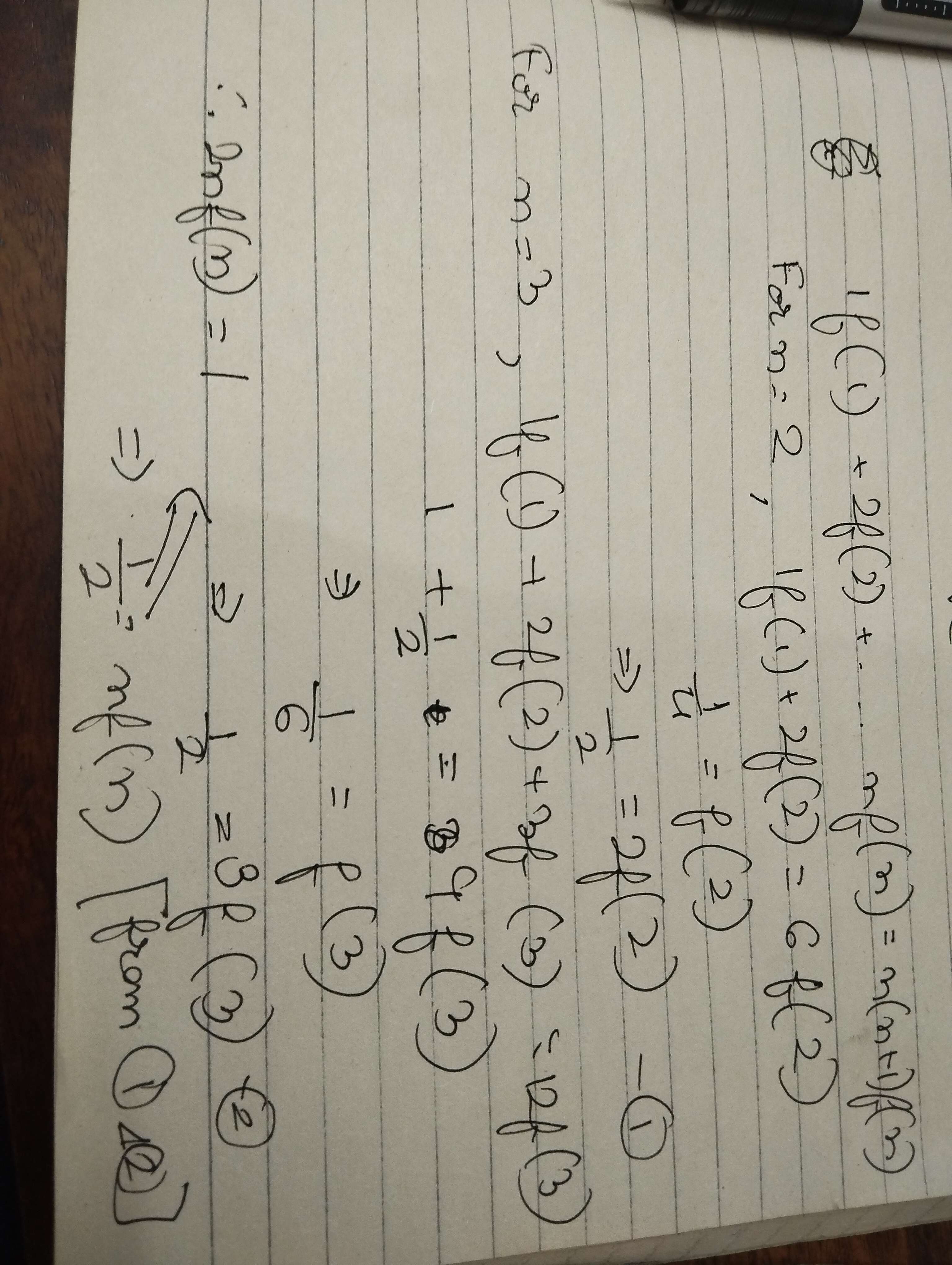28 Replies
@Apu
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Q163
Oh wait this had come up a while ago too
Not 161
Mb
Oh nvm
Although I also have a doubt in 161 xD
How do I solve 161 @Opt if you know the method
Ah.
The function might be periodic I think in 161.
Oh yeah it is periodic.
How did you check?
I cannot understand the problem solving approach for the life of me
I know that I have to put some values and that it should be periodic or be in some series because the that's the only way the question would be solvable but idk how to approach this
Consider a quadratic of x^2-sqrt(3)x+1=0 and the value of f(n) are of form a.alpha^n+b.beta^n
Isme quadratic kidhar se aaya 🫠
There is another method for these kinda questions. Look up how to solve simple second order linear recurrences for more detail ig.
A simple way to look at it is this: You know how mewton's formula is proved? Similar kinda thing you have to do to prove the inverse of it.
O I see
However how did you arrive at x^2-sqrt(3)x+1=0 ?
Why this particular quadratic
Yeah. Newton's formula says if f(n)=a.alpha^n+b.beta^n, f(n+1)->x^2, f(n)->x and f(n-1)->constant term gives a functional equation that is true for all n.
I understand the proof of the roots now but I don't understand why this specific quadratic
Isn't that just the converse of that?

I might have made a mistake?
I got a recursion and extended it backwards
Answer is 2

@Fusion 163 or 161??
I'm guessing both.
The question states f(n+1)-sqrt(3)f(n)+f(n-1)=0 right?
Both
So, lets say you had a quadratic x^2-sqrt(3).x+1=0
Yee
Ah ok
And f(n)=a.alpha^n+b.beta^n where a and b are constants and alpha and beta are roots of the quadratic.
Wouldn't that satisfy this? (proof similar to newton's formula)
Yup. Got it
Never tried to think this way
Thank you too opt
+solved @SirLancelotDuLac @Opt
Post locked and archived successfully!
Archived by
<@895699982265511976> (895699982265511976)
Time
<t:1748961495:R>
Solved by
<@1075951732460376214> (1075951732460376214), <@763645886500175892> (763645886500175892)