Functions doubt (Q166)
I don't understand how to approach the question.
How do I make use of the information that f(x) is symmetric about x=a?

25 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.,rotate
So, if f(x) is symmetric about x=a then going x distance from both ends of x=a would yield the same result and since fxn is odd,
f(a-x)=-f(a+x)
Is this how I'm supposed to solve?
No, f(a-x) = f(a+x)
f(0-x) = -f(0+x)
It's not odd about a
f(x+a)=f(a-x)=-f(x-a)
It's even about a, odd about origin
OH I see
from this, f(x+a)=f(x-3a)
That didn't strike me until you pointed it out for some reason.😓
Hence the function has a period of 4a.
I'm confused now what
Where did you get 3a from?
f(x+a)=f(a-x)=-f(x-a)
f(x+a)=-f(x-a)
Now put x+a=t-a
f(t-a)=-f(t-3a)
Subtract the equations to get f(x+a)=f(x-3a)
Henceforth, f(t)=f(t+4a) and hence the function is periodic with period being 4a.
Ah I see.
Also I think the question should have f(1+4ar) rather than 4r.
Can you pls explain the -f(x-a) part pls
The function is odd hence, f(a-x)=-f(x-a)
Subtract which eqns?
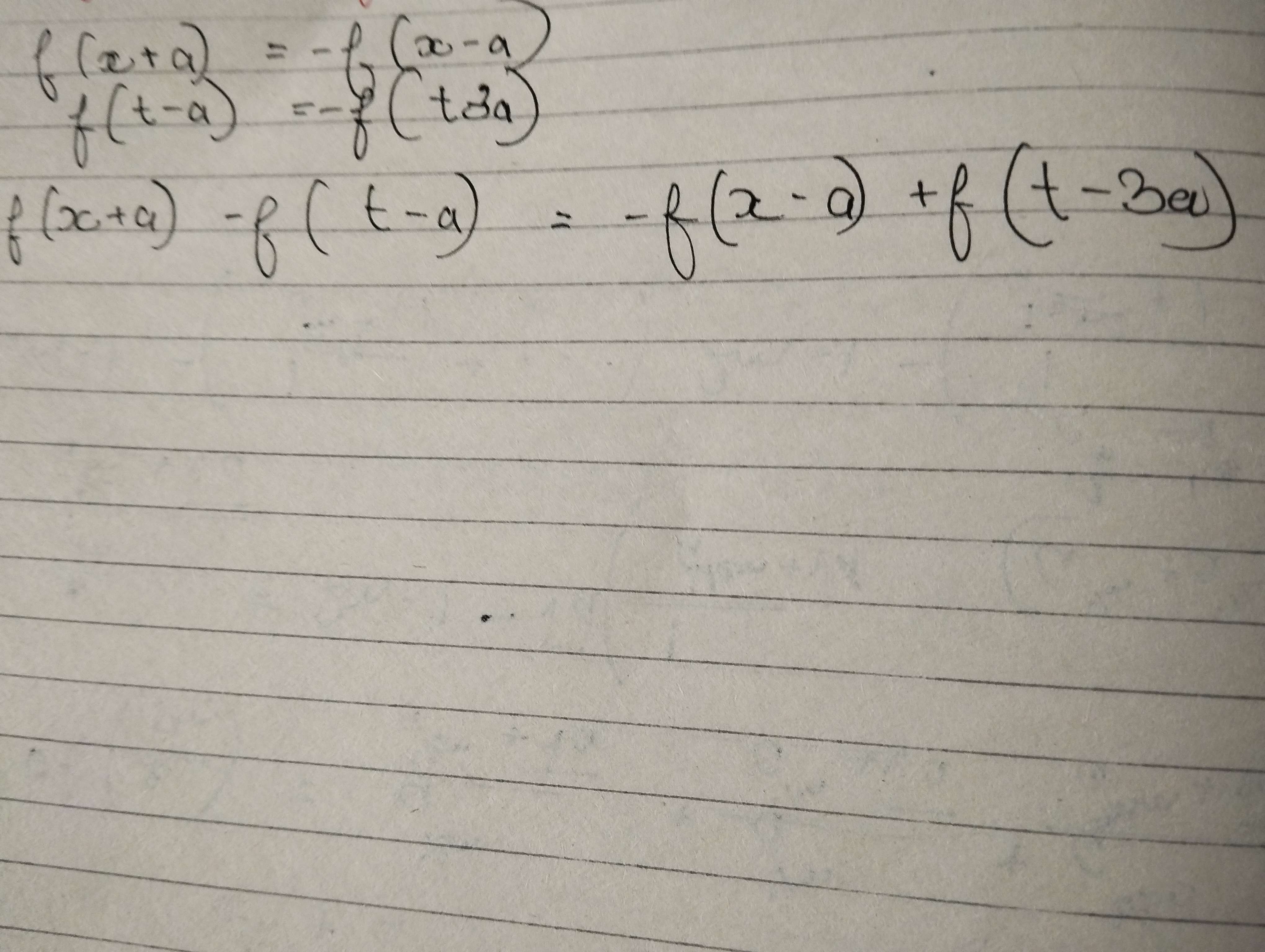
@Opt pls help
f(x+a) = -f(x-a) (eqn1)
As Lance said, replace x by x-2a
f(x-2a+a) = -f(x-2a-a)
f(x-a) = -f(x-3a) (eqn2)
From eqn1 and eqn2, we get that
f(x+a) = f(x-3a)
Now replace x by x+3a
f(x+4a) = f(x)
@Fusion got it?
Yupp
Thanks
I got confused by the t substitution that lance used even though I shouldnt have
Thanks Bois
+solved @SirLancelotDuLac @Opt
Post locked and archived successfully!
Archived by
<@895699982265511976> (895699982265511976)
Time
<t:1749016936:R>
Solved by
<@1075951732460376214> (1075951732460376214), <@763645886500175892> (763645886500175892)
Oh make sure you're comfortable with variable switching. It's going to mess with you otherwise.