10 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.bro what are they doing here
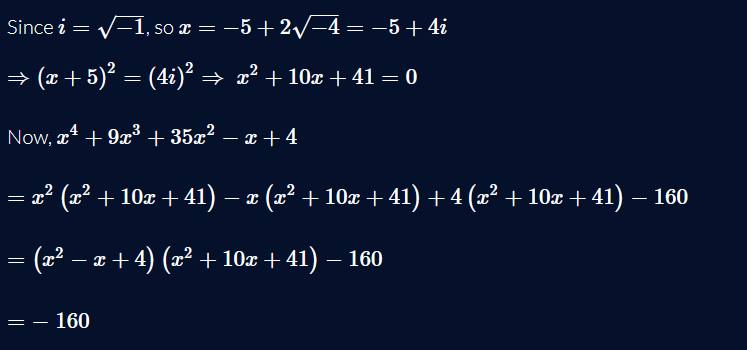
what is that
Let there be a polynomial with one root as -5+4i.
For coeffecients being real its conjugate must also be a root of this polynomial.
In line 2 we find the said polynomial.
Now, let q(x)=p(x).r(x)+g(x) where p(x) is the polynomial we found in 2 and q(x) is the biquadratic we have.
Plugging in the complex number in q(x), the p(x).r(x) term becomes zero and the remainder, g(x) gives the requisite.
what is this step
why'd we do that
Remainder theorem kinda stuff.
ouh
i completely forgot that existed
Like jabh degree greater than 2 hoti hai, this is an approach.
uhh
oke well
ill do remainder theorem
and some questions
then see if i get this better
ill close it then
thank u