functions
here instead of |x| shouldnt it be |x-1| and 1-|x-1| intead of 1-x and so on? since that x was for f(x) whereas we're dealing with f(x-1) now


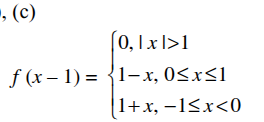
21 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.@Fusion hi am i right
Not necessarily
1-|x| for all |x| <= 1 implies that x lies between -1 and 1
Similarly you can make cases for the other inequalities
where f(x) = 1-|x|, |x|<=1....doesnt this imply that the argument in the function is x
so f(x-1) would have 1-|x-1|
Yes
I looked at the soln and ye, its incorrect imo.
Also, you couldve solved this with a graph. That wouldve been wayy quicker
@Opt can you confirm once?
graph is the last step here, no? after defining the function in the intervals we see where it intersects
ye
yeah so the right ans would be only (a) right
yup
I can do it, if it's not clear yet
just wanna confirm whether the solution is wrong or im trippin 😭
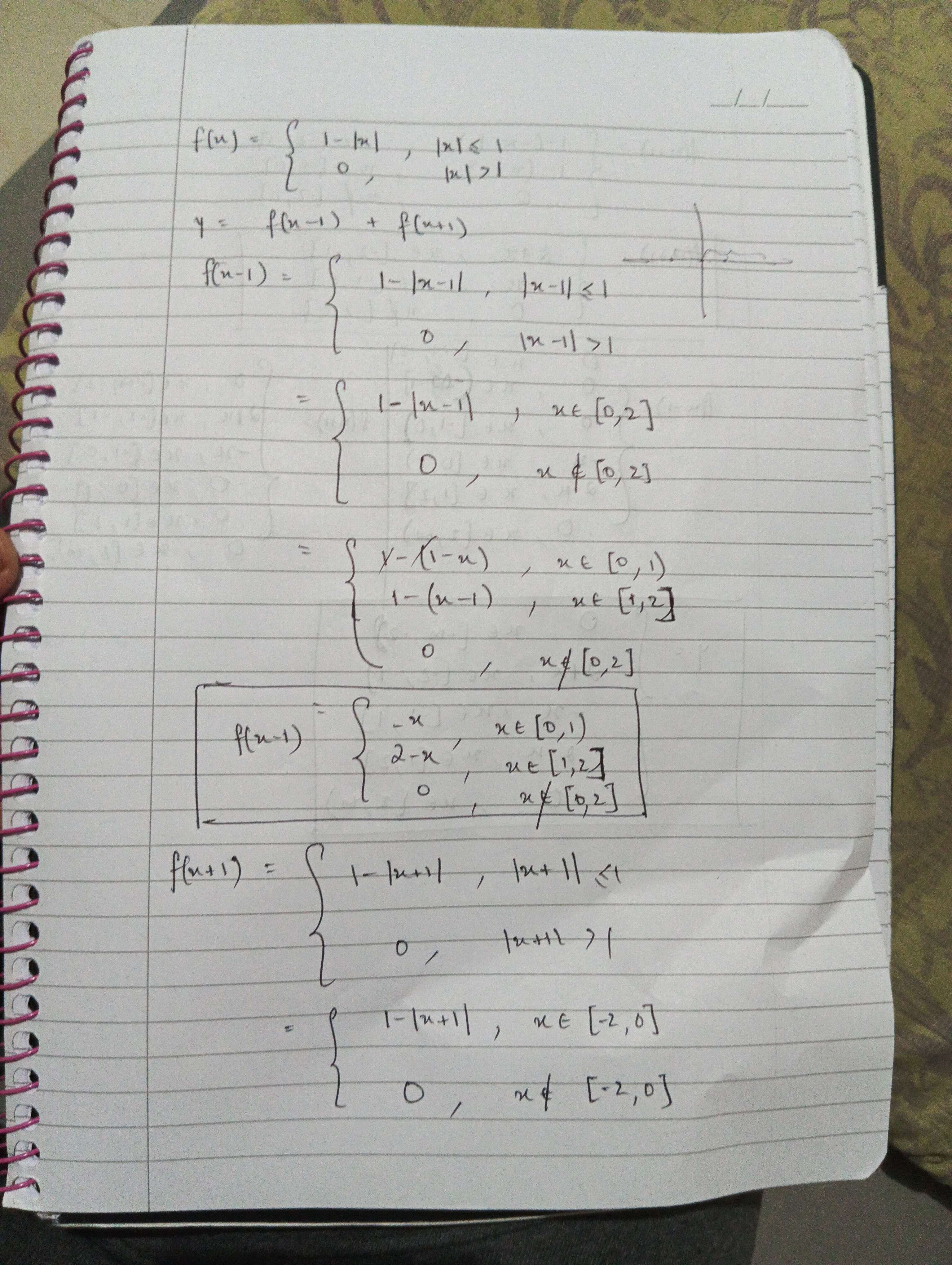

@Augustine here you go, the full working
ohkk thanks
yes the soln is wrong
yepp
alrr got it
+solved @Opt @Fusion
Post locked and archived successfully!
Archived by
<@1199636217302618184> (1199636217302618184)
Time
<t:1749144166:R>
Solved by
<@763645886500175892> (763645886500175892), <@895699982265511976> (895699982265511976)