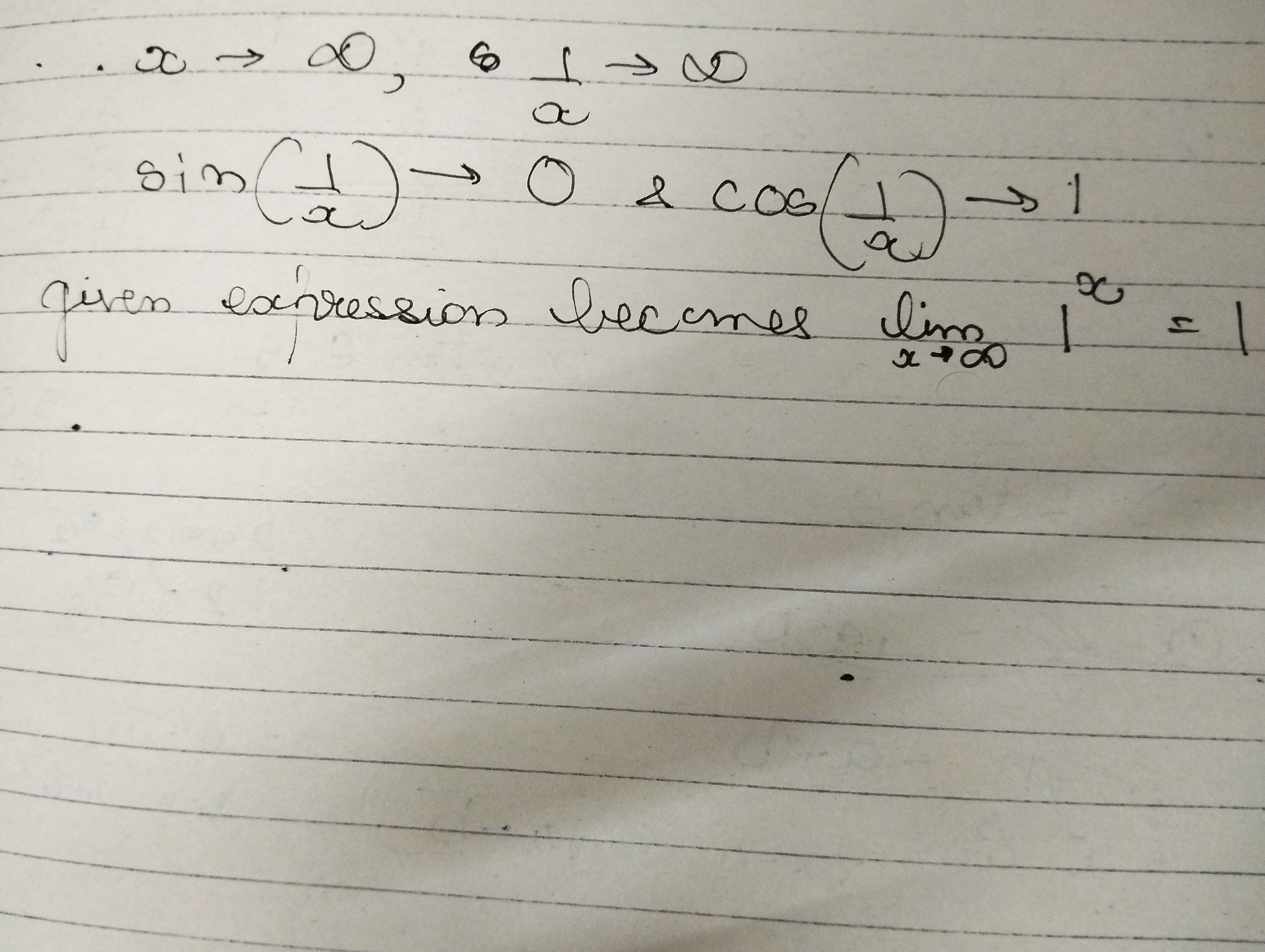40 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.So there's a specific formula for these types of limits

Yours is wrong because you assume the thing inside bracket to be exactly 1
O I see
How would I derive this?
When it's actually tending to 1
Usually you've to memorize this
The limit function is applied so can't I write it as 1
Yes it's not 'exactly' 1
O ye I see now
Alr thanks
Np
Wdym by types
Is this only applicable for 0^infinity type forms?
Check in your textbook
Also opt I'm kinda confused in this shouldn't it be 1+f(x) where f(x) tends to zero,
But here even the cos fn is tending to 1 and not exactly 1
@Fusion
For $1^\infty$ type limits, try using this.
$lim{x\to a} f(x)^{g(x)} = e^{lim{x\to a} g(x)\cdot(f(x)-1)}$
When we have f,g such that $f(x) \to 1, g(x) \to \infty$ as $x\to a$
Opt
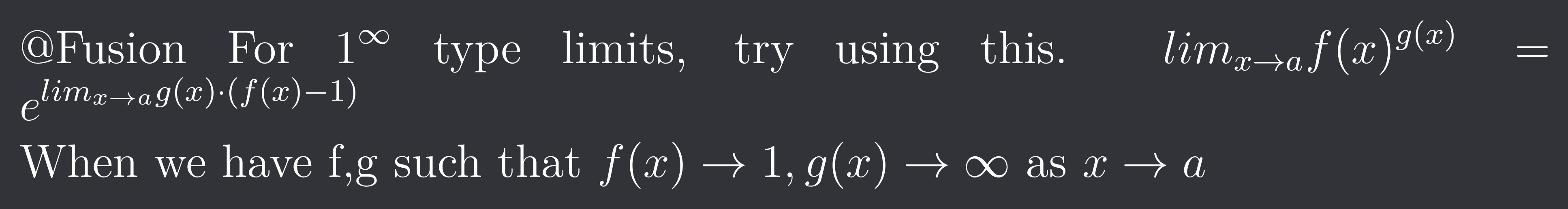
Okay yeah we gotta use this
Mb fusion
The book has used the formula coolguy mentioned
Yeah don't use the one I said that is a different form
How is your formula incorrect
That's the one that the book uses though
It's the same formula
Different format
How would I derive this @Opt I'm wildly confused
I forgot ngl. I remember reading this in some random book and it was useful
I was never taught the derivation
I watched some lectures on limits and I'm still confused on the problem solving part
I see
I remember the derivation for 0^∞
Just do mains pyq and remember diff formats
That's just taking log and exponentiating simultaneously
Alr
Do you have a formula sheet for formulae like this?
Because these aren't in arihant (the book I'm using)
Arihant is a great book it must have
It doesn't have these formulae though
Lemme chk
It isn't under the limits chapter and functions chapter atleast
Only expansion formulae are given
And tbh you can note these formulae as you study in a diff nb, there aren't a while lot
Right
Oh alr I'll do that then
Thanks again
Anytime
The formula occurs as follows (1+f(x))^g(x) as f tends to zero and g tends to infinity, limits to e^f(x).g(x) (This occurs due to taylor expansion of (1+ax)^bx)
Oh wait, I pinged the wrong person
@Fusion
Thanks
Welcome 🖖
+solved @coolguy. @Opt @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@895699982265511976> (895699982265511976)
Time
<t:1749444101:R>
Solved by
<@765933523705921606> (765933523705921606), <@763645886500175892> (763645886500175892), <@1075951732460376214> (1075951732460376214)