12 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.@Nimboi [ping if answering] I think after finding t you can find any one dist to get focal dist
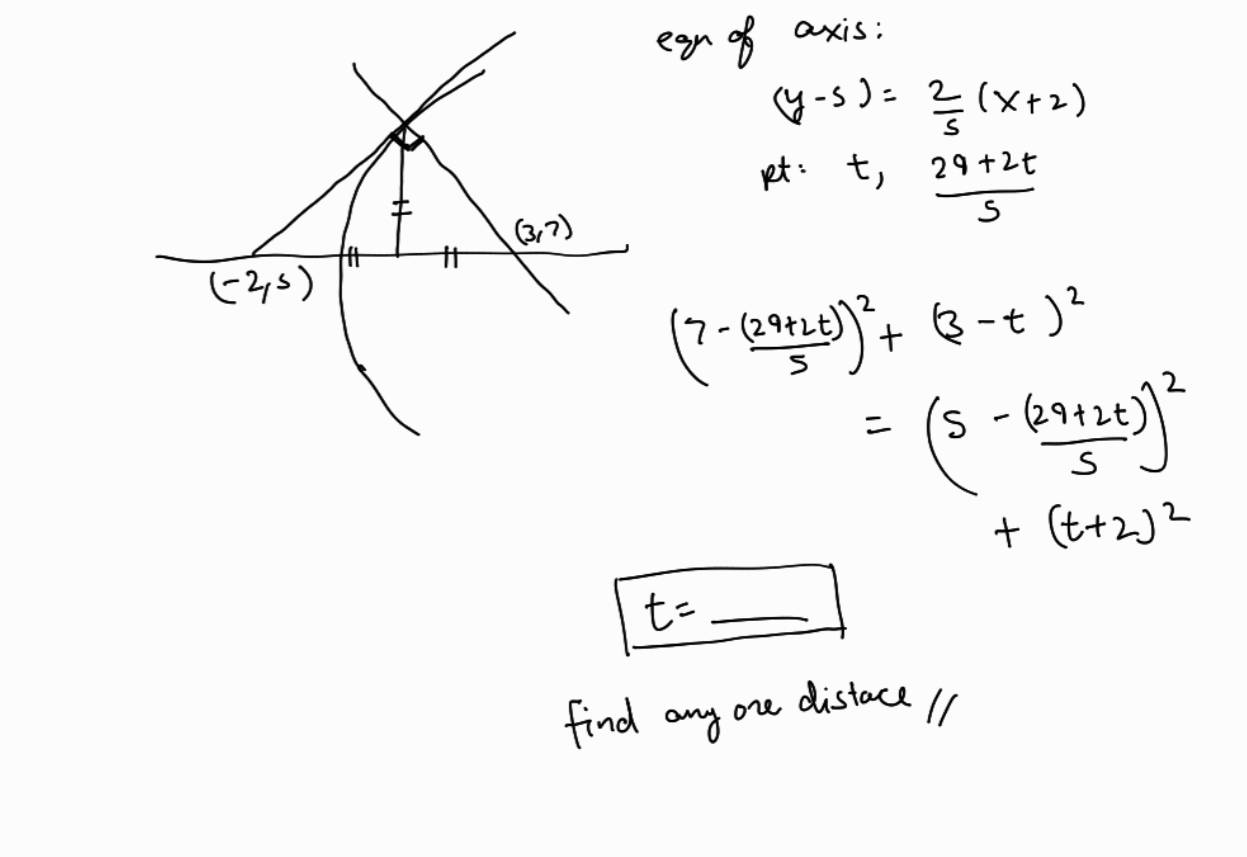
You'll need to know this property though
ah hang on, what property did you use here?
Basically those base angles of triangle 1 are equal and base angles of triangle 2 are equal - cengage gives it clearly
alr ill look it up in a bit
so any point's foot of perpendicular on the axis is the midpoint of the foot of the tangent and normal?
that's a really interesting symmetry
It ain't foot of perpendicular see carefully
oh mb
assumption baseless
Isokay
ah
+solved coolguy.
Post locked and archived successfully!
Archived by
<@759051317124792351> (759051317124792351)
Time
<t:1749882584:R>
Solved by
<@765933523705921606> (765933523705921606)