34 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.I did until this

should i just substitude the accleration values
and equate?
ans kya hai?
b ig
yea option b
anyone
You are approaching right
Just find the initial velocity of ascent and then equate the heights to get the ratio
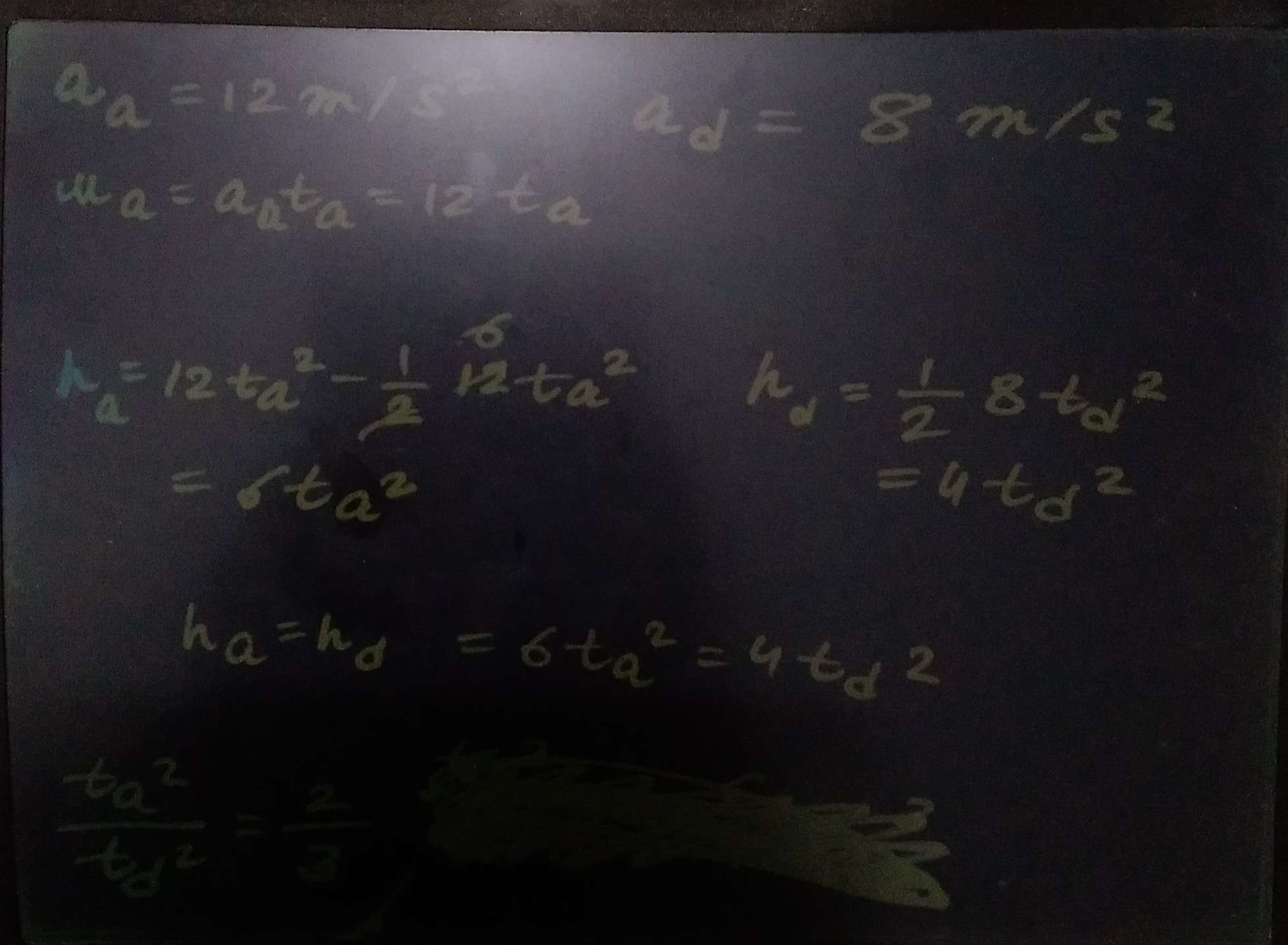
As the object is going up, there is a retarding force that is opposing the action, so the acceleration of ascent will be be -ve
can u explain what u hav done in second step
ua one ??
i get it but what about the negative sign
like
-(g+a)
accelration negative?
do u know sign convention?
yea
but my q is
when body is going up its accelration due to gravity and air resitance gotta be negaive right
correct me if im wrong
Yep
so isnt it -12m/s^2
It is
yes
it is
but u wrote it as + in the img
in the eq ut + 1/2at^2
instead of u, u substituted at i get it
its - only ?
the eq is 12t^2 - 1/2*12 * t^2
y isnt it -12 at start
As we go up, at the maximum height, final velocity is zero and the acceleration is negative
So, 0 = u - at
so u = at
Yea
so the formula became at^2 + 1/2 at^2
For ascent, it's ut^2 - 1/2 at^2; and for descent, its 1/2 at^2
yea
sry i get the point now
but a is -12 right just confirm me that
for asscent
Yea
k
and substituted u = at eq in the ascent eq right
Yea
thx
+solved @Prachi @YesArnavPie123
Post locked and archived successfully!
Archived by
<@1354810703004831746> (1354810703004831746)
Time
<t:1749558810:R>
Solved by
<@926887811674673172> (926887811674673172), <@885013580024528941> (885013580024528941)
