100 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Ok, so, what defines parallel and series is if whether the potential difference across or the current through the components is the same
Not kidding
A friend of mine is asking me “exactly” the same question rn
In my dms
can we like 😭
Trying to explain to him
this is og question i think
Now, the current (charge) through the capacitors is not necessarily the same, because there are other pathways for the charge to flow, and not just in a straight line through the capacitors
Maybe @Opt ka view point dekh ke use better samjha paaun
However, if we consider points connected by straight wires(ideal conductors), they must be equipotential, since charge will flow until the two points become equipotential.
i dont understand this heavy language 😭
Ok ok, I'll explain in simple terms
thnks
Because there's a straight wire from A to another point (I'll call it point 2), both the points are at the same potential
Got that?
Same logic applies to the straight wire from B to Point 1
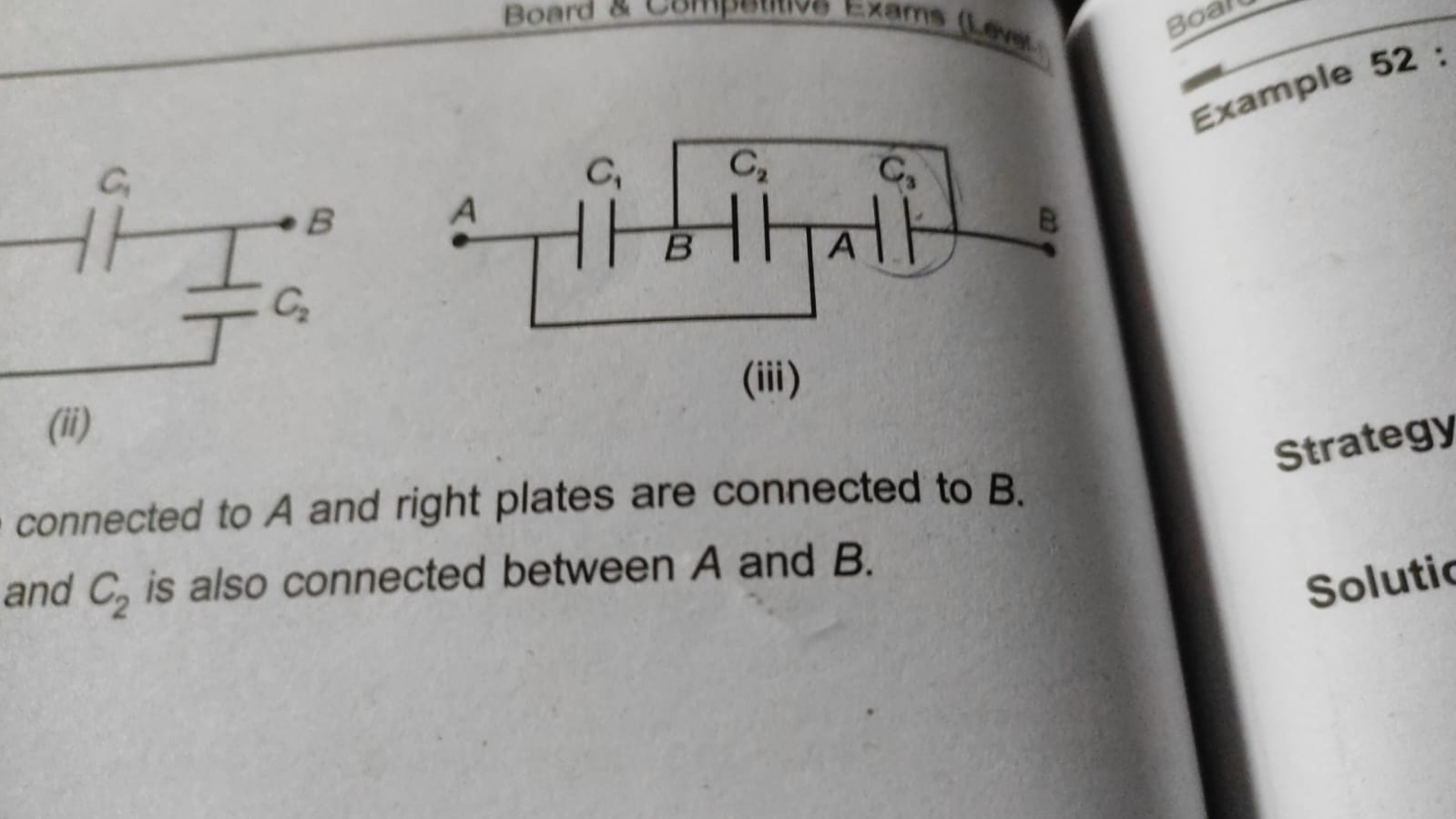
wait wait like in between which capacitor because 2 a are there
I can't draw rn so I'll write.
A C1 P1 C2 P2 C3 B
Is the diagram
A and P2 are connected by wire
B and P1 are connected by wire
So, A and P1 are made equipotential
B and P2 are made equipotential
Uh uhh
ok
i kinda get it
So, that essentially means that we can call P2 A, and P1 B. That's the thing that they've done here
Which weirds people out unless you're writing it on a board
And showing what you're changing
so before the c1 the potenital is same as between c2 and c3
right?
exactly
Now, I’m not getting this which I apparently was a few moments ago
Yeah the potential across each capacitor is V(A)-V(B)
Sorry 🙇
Will try coming up with something
Nahi to will dm you if that’s okay
half got it half not
Ok, seph ji, one last thing
You got the equipotential thing right?
ys
two surfaces which have same potential
in this case the points named a have same
and same on b
So, C1 is connected between A and P1, but P1 is equivalent to B, so why not just connect it to B instead?
C3 is connected between P2 and B, but P2 is equipotential to A, so just connect it to A instead of P2
C2 is connected between P1 and P2, but those are the same as B and A, so just connect it between B and A
What do you end up with?
Three capacitors connected in parallel between A and B
yh
i got this yh
but hre it says in book
that c2 nd c3 are in series
One question
How do you explain that “physically”?
Solving it is one thing, we have this workaround
The logic is, "All we care about is potential. So if two points have the same potential, then changing connection of a component from one to the other makes no difference."
dont confuse me more
No they aren't.
Yeah it doesn’t that’s fine
The circuits are equivalent
But how does the circuit physically work when the connections are not changed
book has it
wait i will send thier explanation
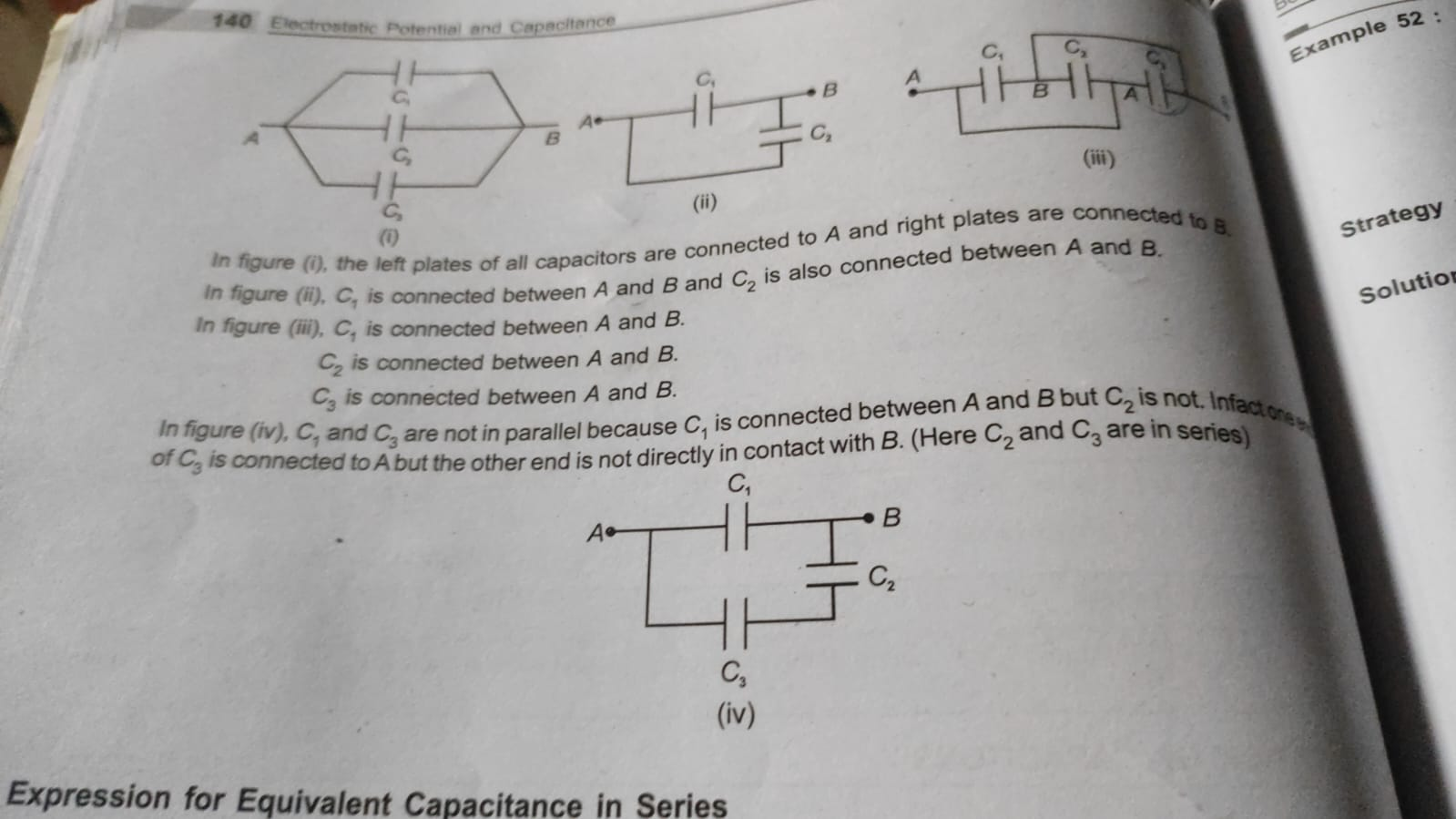
(Of course I’m talking about changing the diagram as per our convenience)
one sentence says it is connected
one para later it isnt wth book
That is uhhhh not right
😭 blame aakash
similar one i dont understand
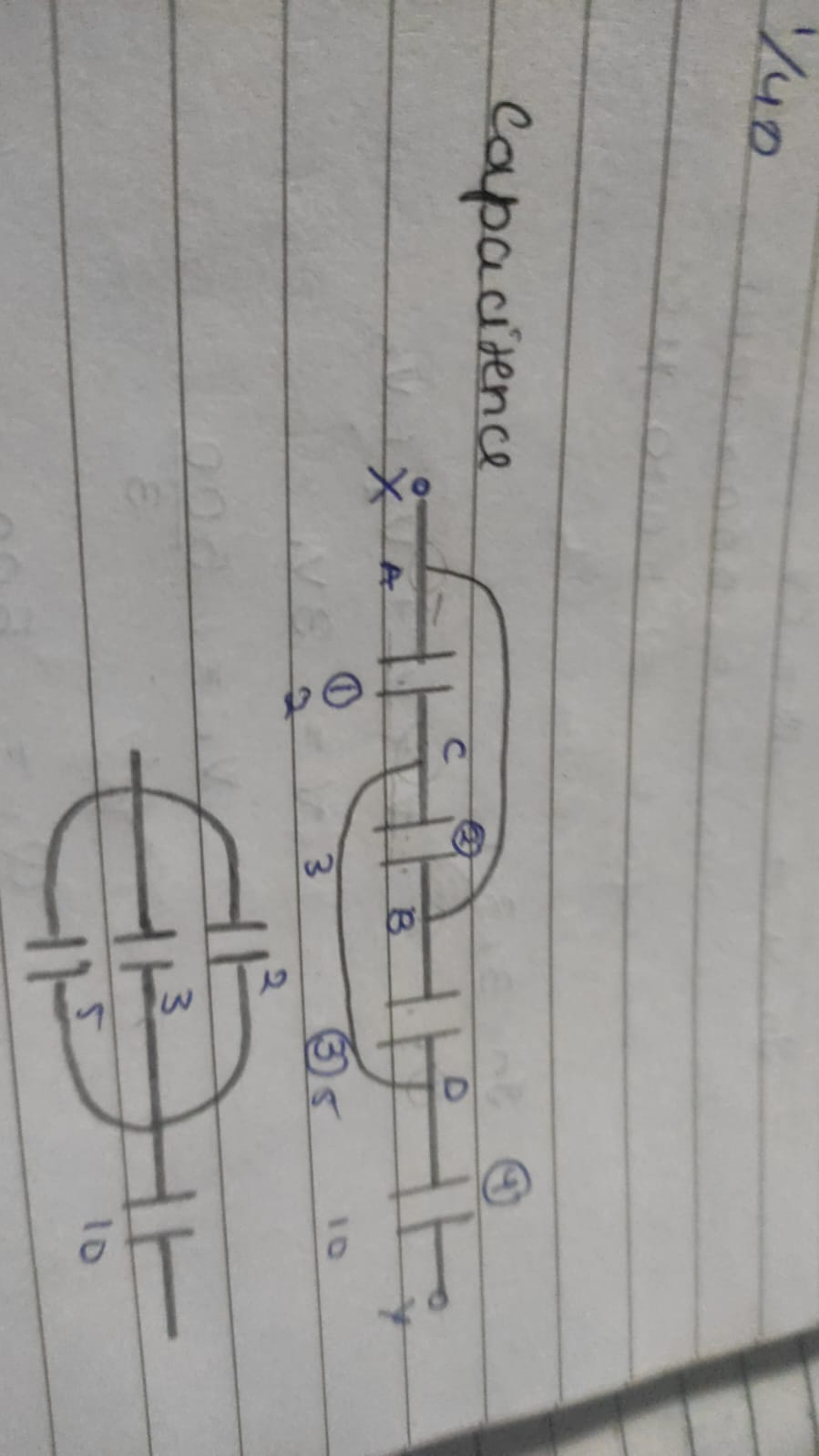
pls help here too
@Opt
the upper one
,rotate
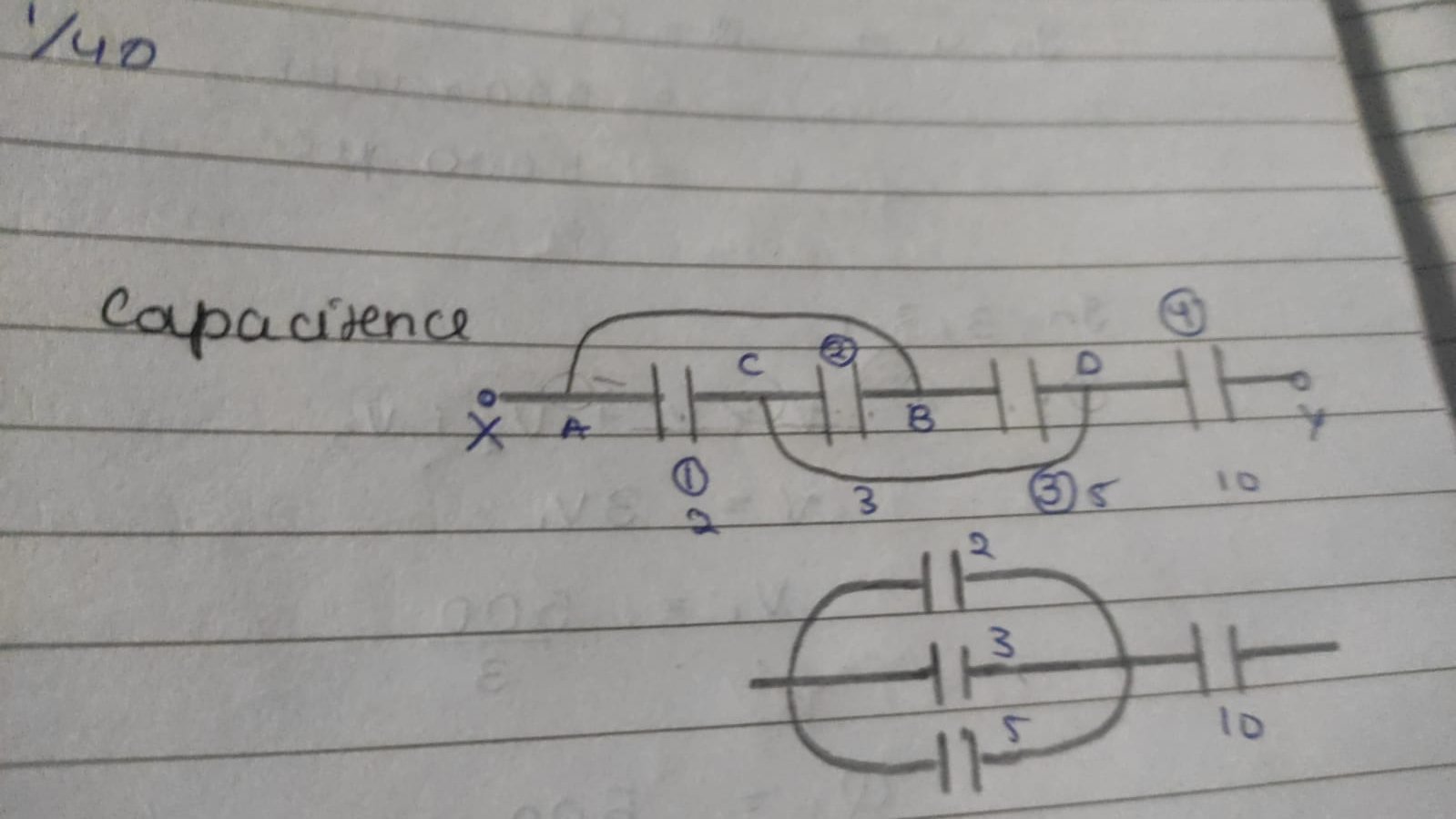
@Opt you got something on this?
Uhhh yeah, but it's tedious to type
It's just charge induction
A lot of it
Trying to visualise it but really weird
Yeah
Was trying to figure out the same in the case of resistors
Because the wires in the middle make it so that charges can flow out of the system too
I ain’t thinking in terms of capacitors for ‘cause that’d be the same
Then it's just Ohm's law
what
I mean how do you physically make the current go through a wire where there is no potential difference
That's the neat part, you don't.
So youre saying
It goes “straight”?
kisi ko pta hai kya 😭??
I don't have pen and paper on me
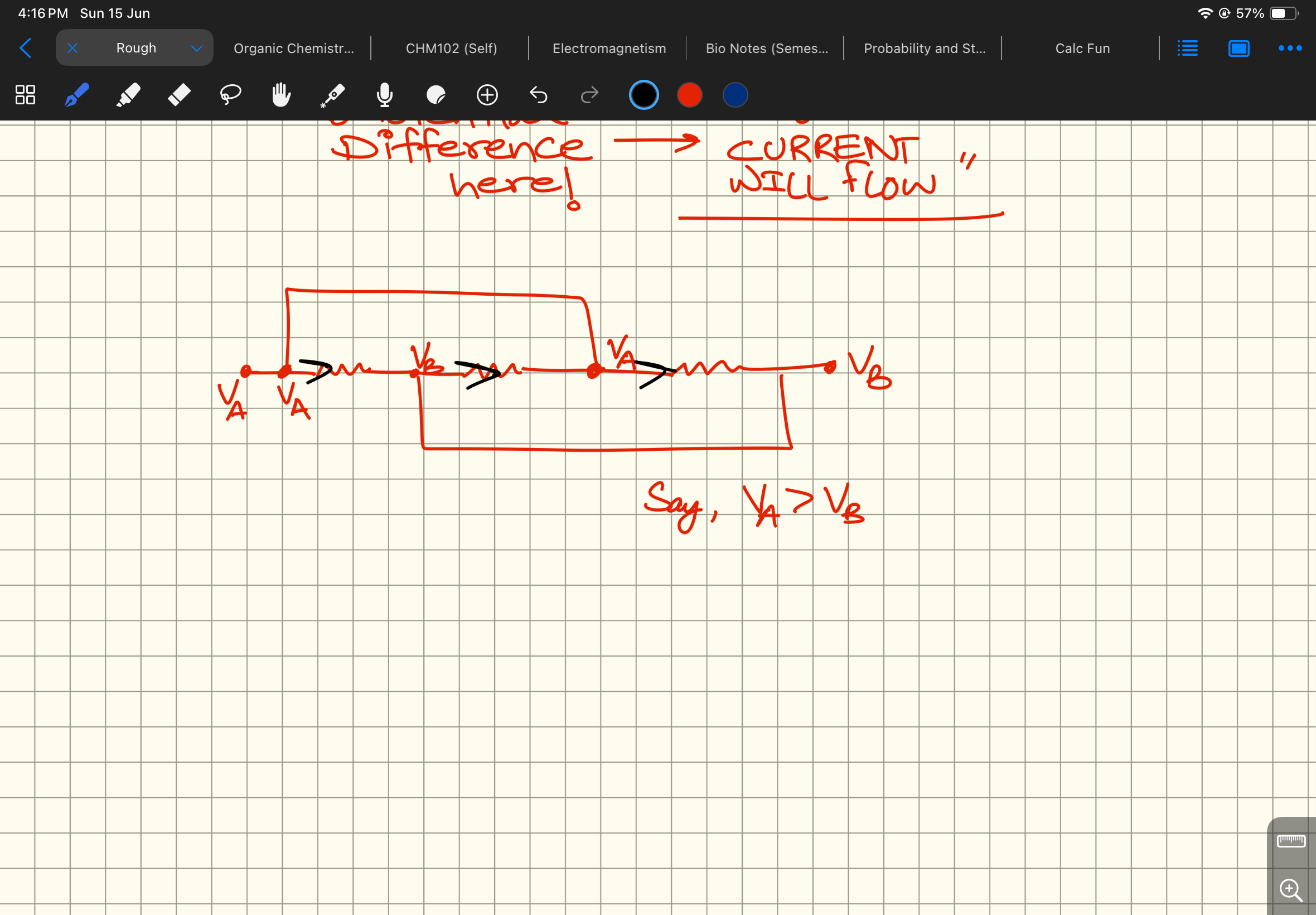
In this case @Opt
can u like do it later and send it later?
How do you go from Vb to Va then
Ah, ok, see no.
That one’s easy I’ll do it in a bit wait
You can imagine that higher voltage means a greater collection of charges. So there's clusters of charge at points at VA
Alright
Then
How do they exactly move?
And charges will try to flow to a less dense cluster
Which is VB
For the leftmost cluster, it has to go right
Yeah
For the middle one
For the cluster in the middle, it can flow left, or flow right
So it does
Once it flows left, it can, without any resistance just go to the rightmost point
So it will do that instead of taking a path with a resistance
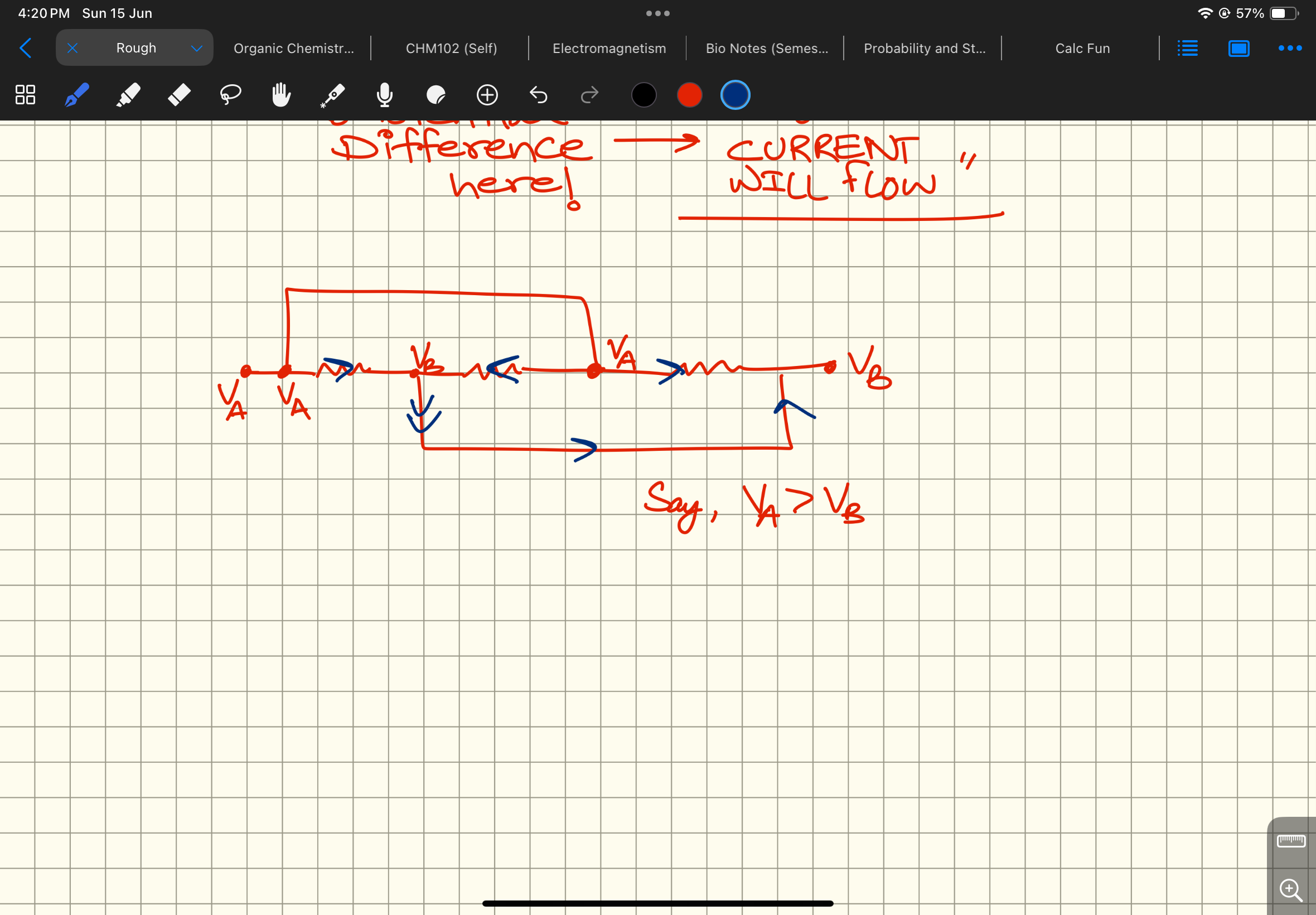
Is this what you mean?
@Opt
Yup. Bingo
Ohh alright fair enough
Thanks for that one
Learnt something new today I didn’t expect
Np np
Btw out of context
Ye
You checked something about the cyanide?
Oh crap no. Lemme go do that. My clayden pdf needs to be redownloaded
I digged and now I’m questioning the pka or water
Dug*
Clayden won’t give you much I guess I checked it
Maybe I’m wrong too so do check it out as well
Nvm that has hard and soft nucleophiles, not acid-bases
Yeah
We could get some idea seeing how it explains cyanide reactivity though
clayden phy me kaha se aa gya
Hum kuch or baat karne lage the lmao
damn this is some crazy ass thing, this is in neet module? @Sephrina
yss
Not really crazy ass tbh
Comes in neet usually
Just the actual explanation is not focused on much
what to explain in this, why they are in series?
i have same question
They arent in series
All of them are in parallel
aren't these all are in parallel?
my book says otherwise
you are seeing answer of fig 4
you asked fig 3
fig 3
tht is simplified form of fig 3 acc to book
Glt ha book mei likh rkha
are dhyan se dekho
sahi likha hai book mai
aur ye doubt hum 4 din se kar rhe hai
naya chasme lene ke baad bhi
aise kaise chalega didi
vahi mai soch rhi
phy gives me existential crisis
faltu mai opt pareshan ho gya XD
varun bhi
close kar do isko abb
dm karr dungi unko
Real😭
+solved @Priyam Alok @Enamine @Opt
Post locked and archived successfully!
Archived by
<@888280831863451688> (888280831863451688)
Time
<t:1750094191:R>
Solved by
<@582564114631491605> (582564114631491605), <@984016629119713290> (984016629119713290), <@763645886500175892> (763645886500175892)