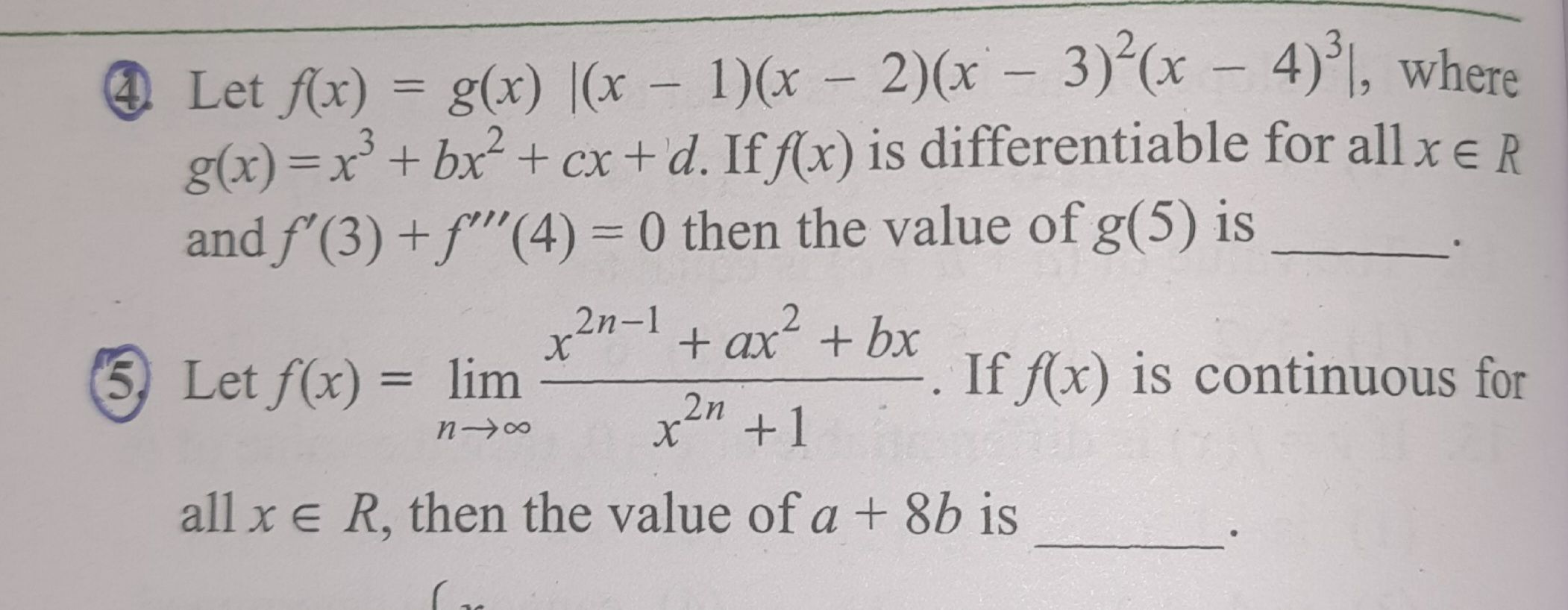7 Replies
@hardcoreisdead
@SirLancelotDuLac
maths hi tohkharab hai meri 🙏
4 or 5?
both
where are the math doubt solvers bro 😭
Well, for the fifth one. If |x|<1, the high power terms of x tend to zero and you're left with f(x)=ax^2+bx if |x|<1. If |x|>1, the high power terms of x dominate hence your function tends to 1/x.
So for f to be continous, f(1+)=f(1-) or a+b=1 similarly for -1, a-b=-1
Also f(1)=(1+a+b)/2=1 which gives a+b=1 and similar for x=-1 [Which also give the above 2 equations]
4th one also seems simple ig. We have to make the above function diff. by removing the mod. Note that (x-3)^2 is positive hence can be removed from the mod. To make powers for stuff inside even g(x) can be k(x-1)(x-2)(x-4). Also note that if g(x) acquires this value, f will have a term of (x-4)^4 that means it does not get removed in differentiating thrice and f'''(4)=0. By a similar logic f'(3)=0. So the required g(x)=(x-1)(x-2)(x-4) [Kind of a lazy method but yeah...]
Will try this fir btata agar hua ya nahi
Hogya bhai
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@1382187168230936577> (1382187168230936577)
Time
<t:1750851145:R>
Solved by
<@1075951732460376214> (1075951732460376214)