24 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.without expansion pls
Have you calculated the limit in the question? (Like the main one)
1/3
jo given hai
so D matches
need to check A and B
Okie.
For a the best thing to use is expansion (same for B)
😭
ok so A mei sirf cos ki lagau ya tan ki bhi lagani padegi
If you don't waana directly do it, use cosx-cos(tanx)=-2sin((x+tan(x))/2)sin((x-tan(x))/2)
So using expansion (x+tanx)/2 tends to x and (x-tanx)/2 tends to -x^3/6
So the overall limit tends to 1/3
tanx ka expansion is...
?
sin/cos toh nahi karna hoa
Its something like $x+\frac{x^{3}}{3}+...$
SirLancelotDuLac
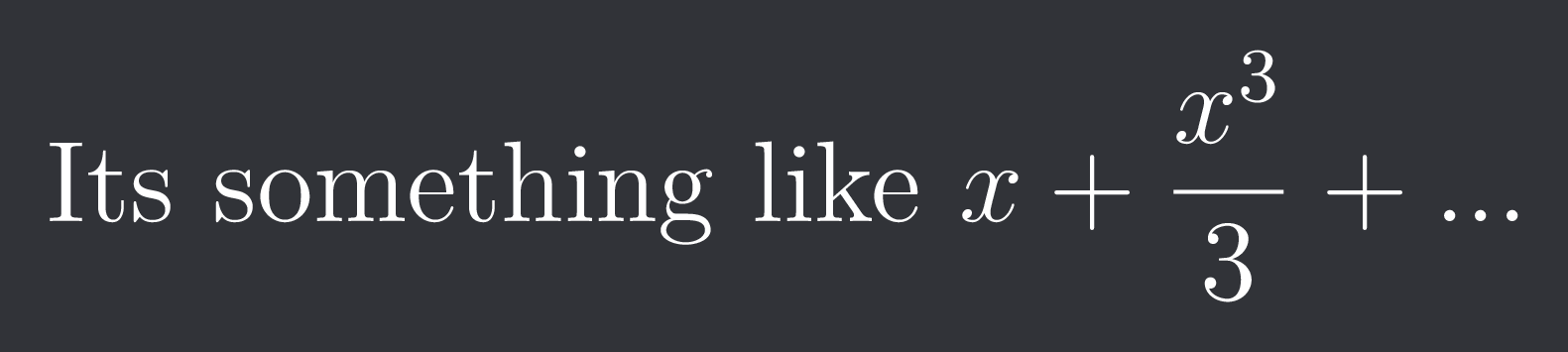
Sort of random ahh stuff so you'll just have to remember 2 (for worst case 3) terms from the start
first 4 terms would be enough to remember right?
For b, simplifying the numerator by taking 9 common and multiplying the power of e to get quadratic in power we get $9(e^{\frac{x^{2}ln27}{27}+\frac{xln(27)}{9}}-ln9)-1$ Note that the numerator tends to zero, hence the whole expression tends to $\frac{x^{2}ln27}{27}+\frac{xln(27)}{9}}-ln9$. Do similar stuff for the denominator to get $27(x-3)ln27$
SirLancelotDuLac
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)

Do check if the tex is correct 😔
But moving on, factorize the numerator and denominator to get the required answers.
can u share written soln of b part
@SirLancelotDuLac
Okie, just lemme find a pen and paper.
kk
In continuation to this (Sorry for the crappy handwriting 😬 but I didn't have a working pen)
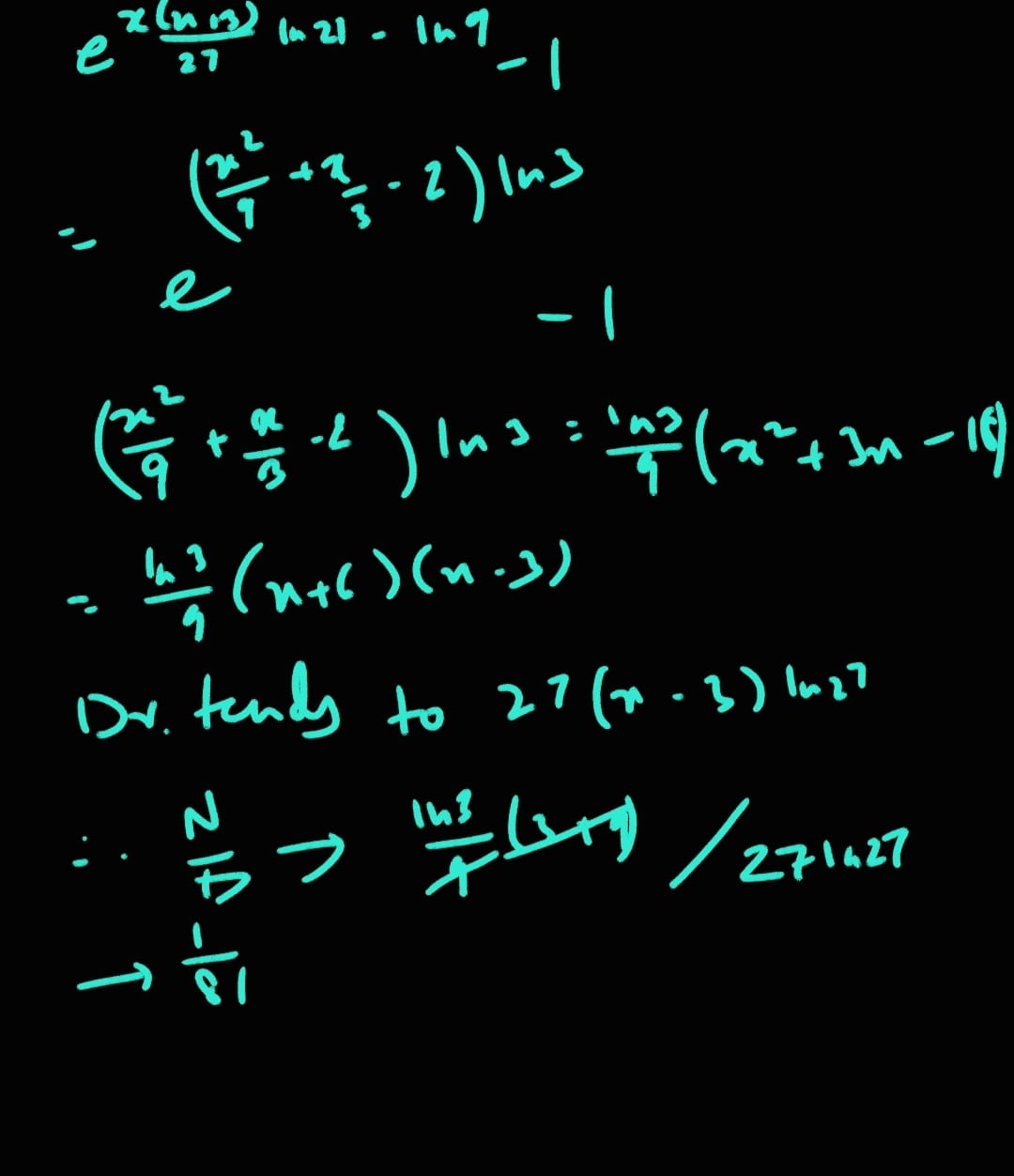
@hardcoreisdead
The written solution. Also mb, it comes out to be 1/3 and not 1/81

2nd se 3rd line pe kaise aaye
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1750927479:R>
Solved by
<@1075951732460376214> (1075951732460376214)