proving inequality w/ mathematical induction
can anyone review my proof for this problem:
https://math.nibirsan.org/posts/proving-2n-n3-for-all-n-9/
15 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.I think something's wrong with how i am using the inductive hypothesis

Wait, how did the log(n+1) become log(n)+log(1)?
sigh
you're right
hotdamn
big, big mistake
hmm i wasn't using the tool properly. i will try a different approach and post the updated proof.
there. i think i am satisfied with it now.
I do not quite agree with this.

a>=b for all n is false, it might be that a<b for some values of n and a>=b for other values of n.
hmm so what you're trying to say is:
$$
\begin{aligned}
&(\forall n>9)[2n^{3}\geq (n+1)^{3}] & \text{- false} \
\implies&\neg(\forall n>9)[2n^{3}\geq (n+1)^{3}] & \text{- true} \
\implies & (\exists n>9)[2n^{3} < (n+1)^{3}] & \text{-true}
\end{aligned}
$$
capn' catto
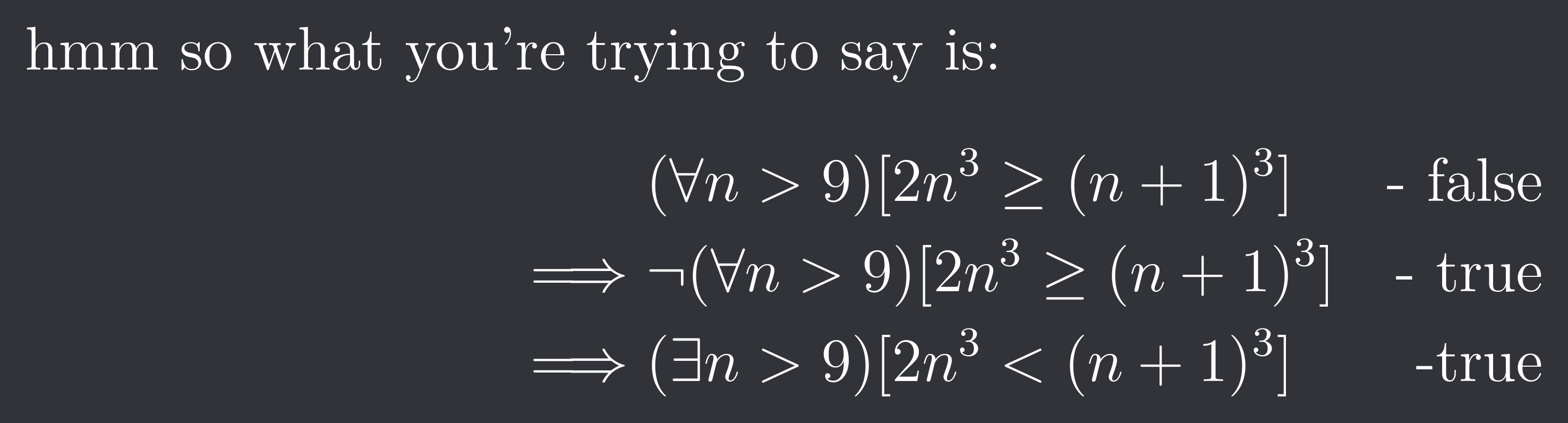
and yea, in that sense, to induce contradiction, i technically need to check for every single n.
which is not really possible,
and without checking everything, this is always a possibility
sigh.
i am stuck.
chatgpt helped me a bit (about the comparision thing), and i got my hands dirty to find some ideas
i think this should be good? pleasee review!
man i learned a lot:
- don't f with log if you don't need to
- get your hands dirty EVEN if it's not a problem to solve
- don't overestimate your abilities (i thought i had nailed things down TWICE)