integration
g'(x) = x^3
integrating both sides wrt x^2 and putting g(1)=1 we get g(x^2) = 2x^5/5+3/5
this gives g(4)= 67/5 which matches the given answer. my doubt is why cant i do
d/dx g(x^2) = x^3
d (g(x^2)) = x^3dx
integrating both sides and putting g(1)= 1 we get
g(x^2) = x^4/4 + 3/4
which is wrong
why??
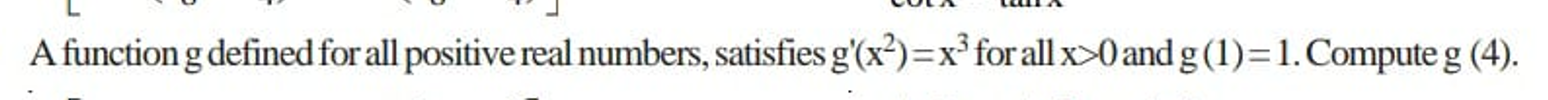
39 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.@Moderator pls ping maths doubt solver
First do the sub t = x² and get g'(t)
Then you can integrate wrt t
Otherwise you have to integrate d(x²)
@Maths Quiz
Wrong one
@Apu
oh okay
mb
thanks
sorry for the ping guys
woh wala part theek hai
why is method 2 wrong
Because $g'(x^2)$ is not $\frac{dg(x^2)}{dx}$.
$g'(x^2)$ means $\left(\frac{dg(t)}{dt}\right)_{t=x^{2}}$
Opt
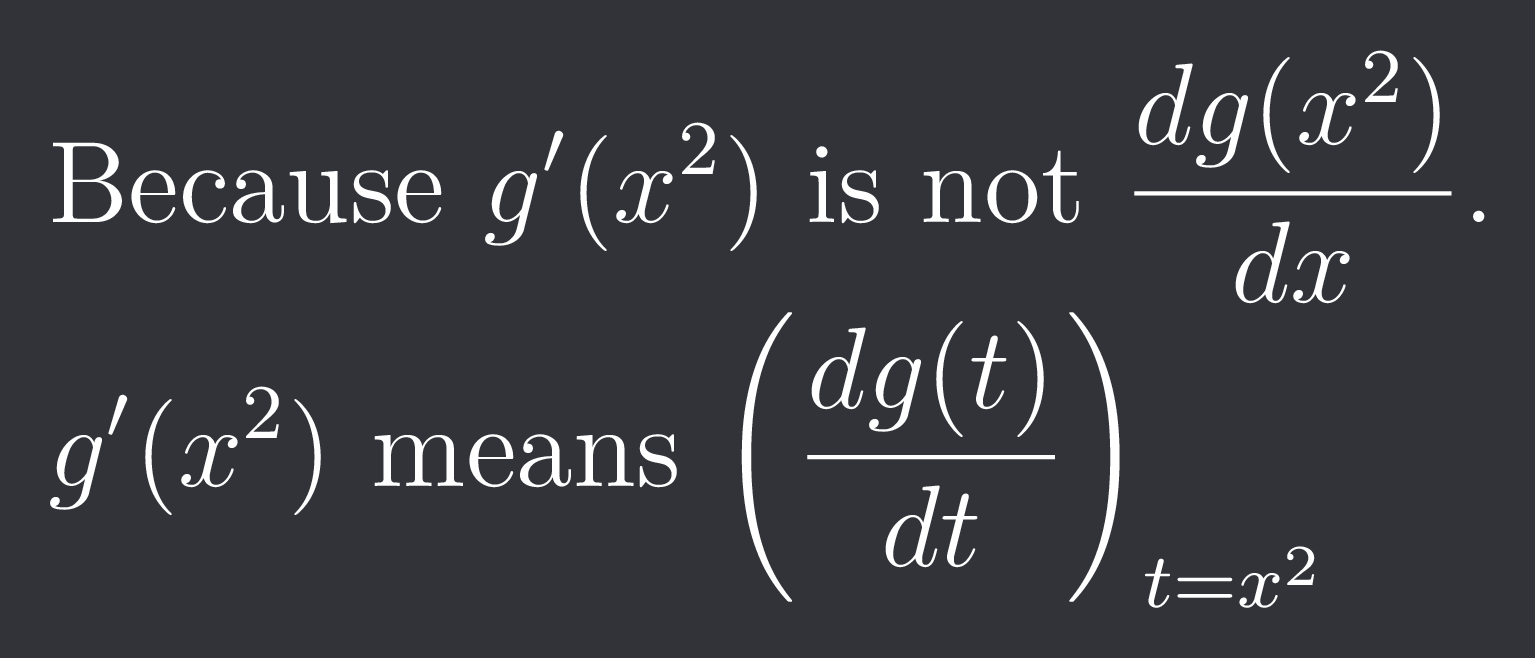
ok so 2=3
1 =/= 2
1 =/= 3

Actually all of them are different.
wha-
lets start with g'(x^2) ig
1. Derivative of the composition g(f(x)) wrt, where f(x) = x², done using chain rule. You get g'(x²) • (2x)
2. Now this is what I wrote in the previous message. It's the function g'(t) evaluated at the square of whatever x value is your input. Note how in 1 there is 2xg'(x²), which means that when you're evaluating it at an x, you need to consider the derivative's value at the square of the x you're evaluating it at.
3. The last one is just your typical implicit diff. It's of the form dg/df, rate of change of one function wrt another, so you can write it as (dg/dx)/(df/dx)
so putting t= x^2 here doesnt give 3rd expression
they might "look" the same but the dont "mean" the same ??
@Opt
Yup
@hardcoreisdead I can give another way to think about it
Forget the x², and just take it to be some f(x)
It makes more sense in the general case
this?
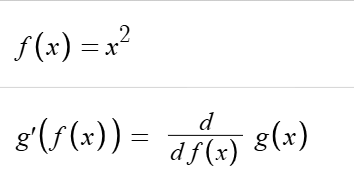
d/dx [g(f(x))] is done by chain rule right? It's the derivative of a composition of two functions.
Compare that with g'(f(x)), which is just a composition of two functions, where the outer function happens to be a derivative of a different function
This is also wrong. g'(f(x)) ≠ dg/df
Lemme find the composition symbol
Compare $\frac{d}{dx}\left(g\circ f\right)$ with $\left(\frac{dg}{dx}\right)\circ f$
Opt
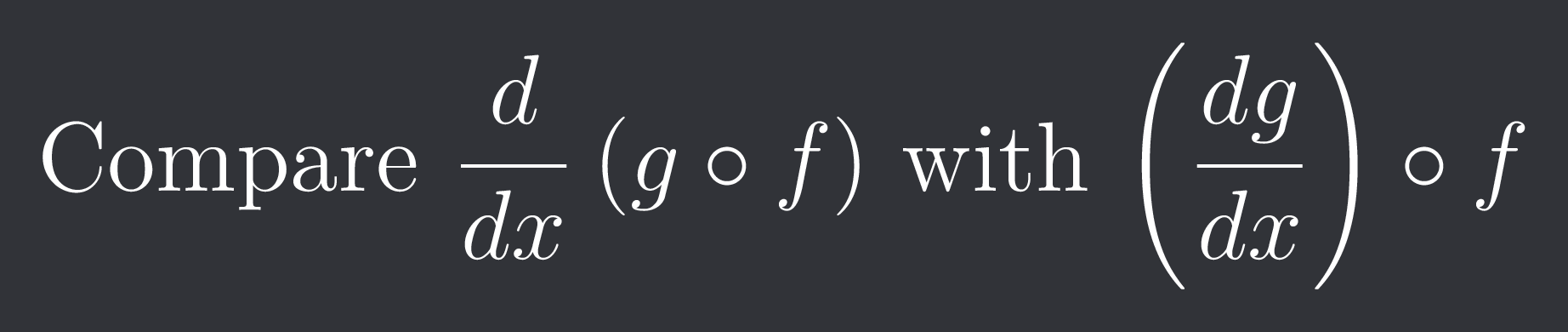
Second one is what g'(x²) means, where f(x)=x²
Ngl, I never thought I'd ever use this circle notation for composition
@hardcoreisdead
isnt this the same of what u said previously. that dg/dt thing just t=f(x)
Look at the most recent one. I realise my previous attempt was also confusing.
Derivative notation is confusing af for no reason
If you want, I'll make one big concise post.
first quantity is g'(f(x))*f'(x)
right?
Yes, chain rule
and 2nd quantity is g'(f(x))
Yup
?
Should I?
g'(x^2) = ( dg(x)/dx (x^2))
wtf is this quantity
wait maybe yhin resolve ho jaye
ughh ill have to go sorry
class hai
It's just a function composition.
kar hi do post
g'(x) ko kuch aur naam do
Say, h(x)
Toh, this is just h(x²)
Consider two functions g(x) and f(x) defined on the real numbers.$\bigskip$
Their composition is denoted by $g\circ f, g\circ f(x)$, or g(f(x))$\bigskip$
By applying differentiation operator onto g(x) and f(x), we obtain two other functions defined on the same domain and range, denoted by g'(x) and f'(x) or $\frac{dg}{dx}$ and $\frac{df}{dx}$ respectively.$\bigskip$
$$g(x)\xrightarrow{\frac{d}{dx}}g'(x)\text{ and } f(x)\xrightarrow{\frac{d}{dx}}f'(x)\skip$$
The derivative of the composition $g\circ f$ w.r.t. f(x) can be simply done by considering f as the input instead of x, and the derivative resulting as such is denoted $\frac{dg}{df}$ or $\frac{d}{df}g(f)\skip\bigskip$
The derivative of the same composition $g\circ f$ w.r.t x is obtained according to the chain rule by multiplying $\frac{dg}{df}$ with $\frac{df}{dx}$, i.e. $$\frac{d}{dx}g(f(x) = \left(\frac{d}{df}g(f)\right)\cdot\left(\frac{d}{dx}f(x)\right)\skip\bigskip$$
The composition of the derivative of g(x), i.e., g'(x) with the function f(x) is denoted by $g'\circf$ or $\frac{dg}{dx}\circf$ or, g'(f(x))
@hardcoreisdead
Opt
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)

so dg/df signfies g'(f(x))
at x
g'(f(y)) would be mean dg(x)/dx at x=f(y)
So this right ?
No, g'(f(x)) means the value of g' function when argument is f(x)
For instance, g=x² and f=sin(x) then g'(f(x))=2sin(x)
Oh nvm, yeah sorry the same thing
got it
@Opt anything to add or should i close
No
+solved @SirLancelotDuLac @Opt
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1751554975:R>
Solved by
<@1075951732460376214> (1075951732460376214), <@763645886500175892> (763645886500175892)