9 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.It's n tending infinity btw
I was able to simplify the summation part up until this
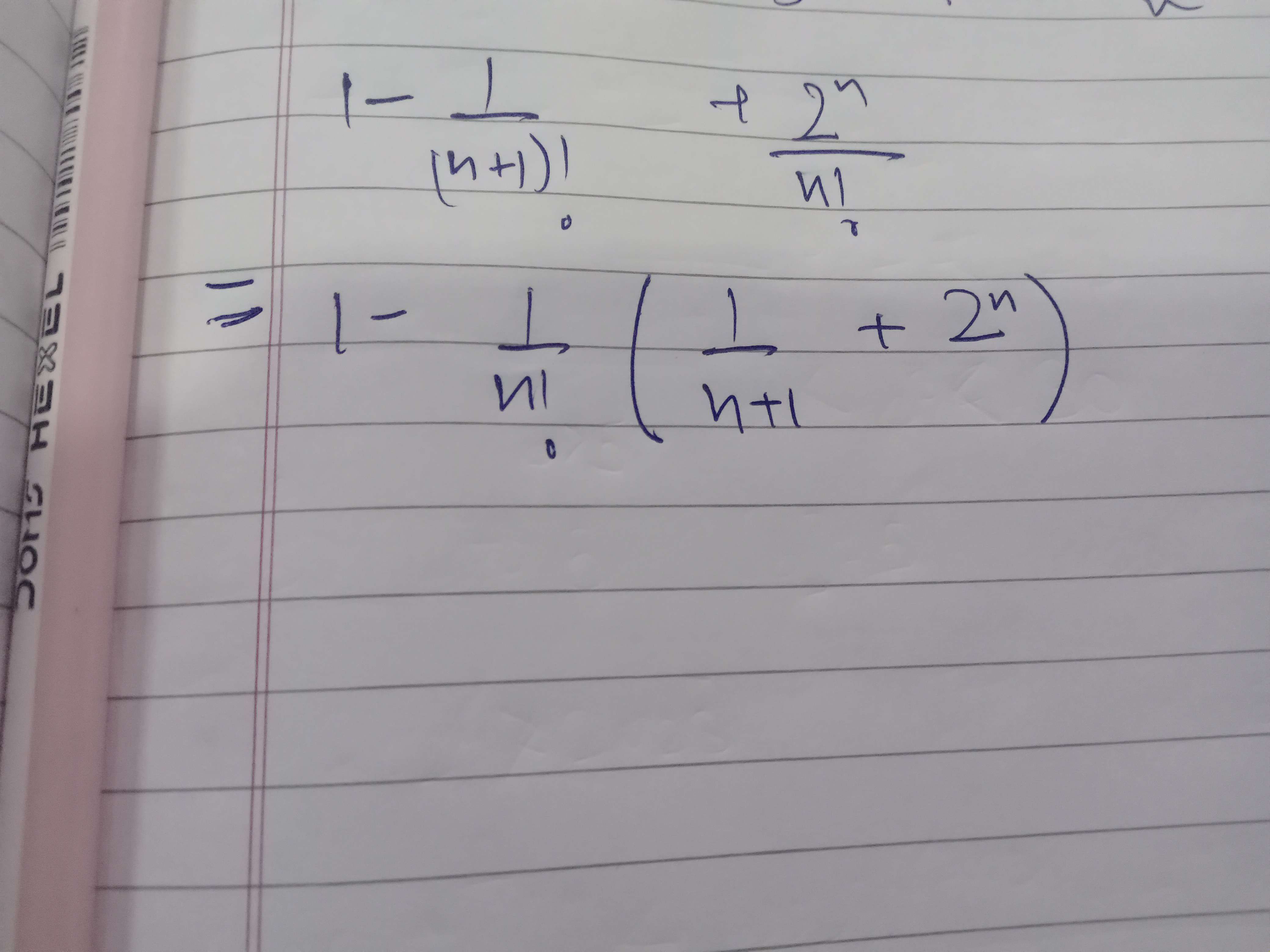
Cant figure out the limit
Everything apart from 1 tends to zero.
Comparing $2^{n}$ and n! would be something like this: $2^{n}$ means that you are multiplying 2 'n' times, while n! would mean multiplying n consecutive natural numbers. Since 3,4....n are greater than 2, this grows dramatically larger than $2^{n}$. Hence the $\frac{2^{n}}{n!}$ wala term tends to zero. As for the $\frac{1}{(n+1)!}$ term that grows to zero.
SirLancelotDuLac

had pretty much the same logic just needed to confirm this
got it
thanxx
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1751551944:R>
Solved by
<@1075951732460376214> (1075951732460376214)
