66 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Where am I going wrong
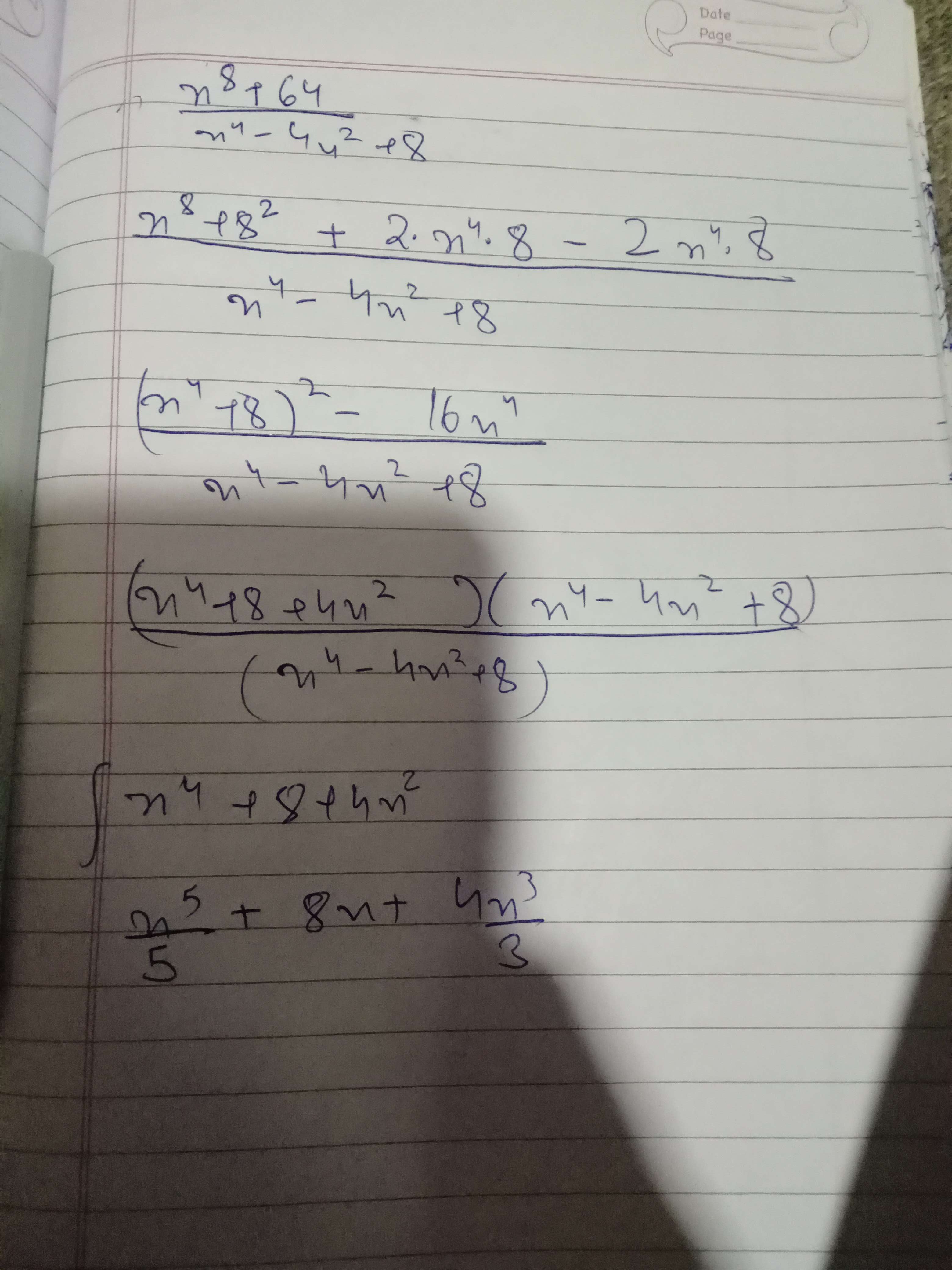
$\frac{x^{8}+64+16x^{4}-16x^{4}}{x^{4}-4x^{2}+8}=\frac{(x^{4}+8)^{2}-(4x^{2}^{2})}{x^{4}-4x^{2}+8}=\frac{(x^{4}-4x^{2}+8)(x^{4}+4x^{2}+8)}{x^{4}-4x^{2}+8}=x^{4}+4x^{2}+8$
SirLancelotDuLac
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)
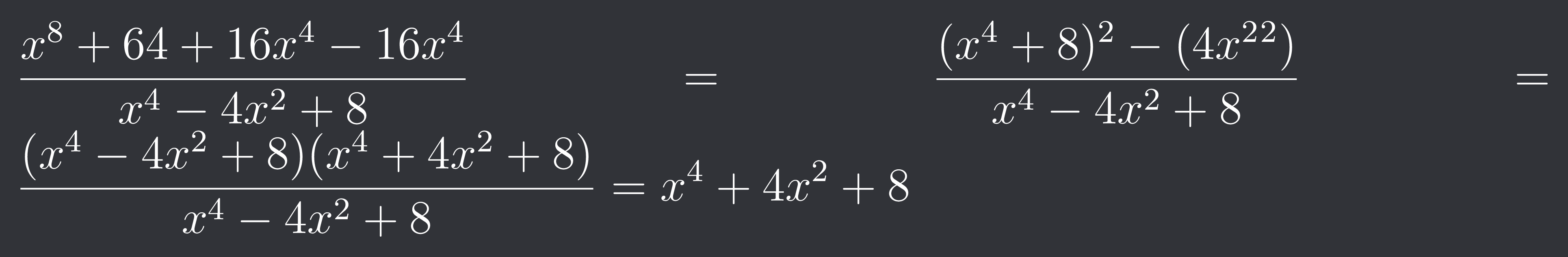
Seems right
Did you check by wolframalpha?
ans key says this
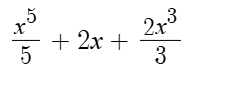
nope
Integrate[Divide[(Power[x,8]+64),(Power[x,4]-4Power[x,2]+8)],x] - W...
Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels.
yep book's wrong
baaki parts ka koi hint dedo
The 8th one is from sameer bansal ig.
Iirc it was some skibidi manipulation...Imma try this once.
alr
Okay nvm, me dumb. The numerator factorizes to $(1+x^{2})^{2}(1+x)$ while the denominator factorizes to $(1+x^{2})^{2}(1+x)^{2}$
SirLancelotDuLac
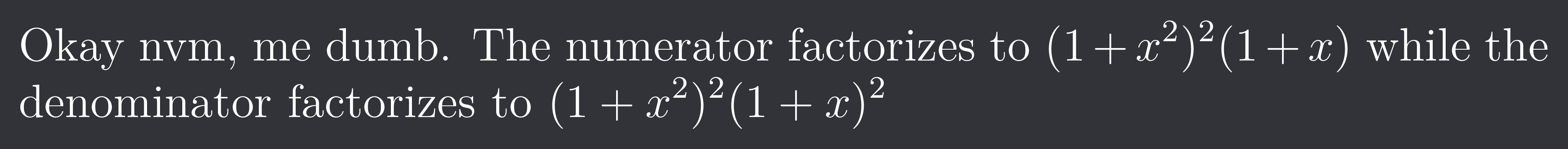
So the answer comes out to be $ln(1+x)+c$
SirLancelotDuLac

how the hell do u even factorise that
nvm imma just do long division
Its helpful to factorize the numerator once and just check, if any factors are cancelling out.
(Which can be done via the factor theorem and shi)
We got Lance saying Skibidi before GTA6
ek aur brainrot shikaar 🥀
yep aa gya . baaki bhi pls 🙏
just some hints
Note that the square of conjugate the expression in the first bracket resembles the expression in the second bracket for the last one
The 9th one seems like some factorization problem.
i am stuck on this part
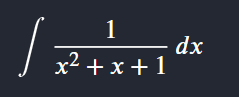
it does resemble but ek ki power 1/6 and ek ki 2/3
This is a standard form. Complete the square neeche to (x+0.5)²+0.75 and then you get arctan((x+0.5)/sqrt(0.75))/(sqrt(0.75))
Nope. First wale ki power is 1/3 hai and second wali cheez ko first expression ka square by 2 likhenge toh we get (first expression times uska conjugate)^(1/3)
yeh kaise standard form hai 😭
how does it strike to do this
Integrals ke types padhate hain na coaching mein?
oh han
wait
nahi idts yeh specific integral cover hua hai
well completing the square it is
@SirLancelotDuLac can u just share last part solutin
For numerator: $(x+\sqrt{2-x^{2}})^{1/3} \cdot (\frac{(x-\sqrt{2-x^{2}})^{2}}{2})^{1/6}=(\frac{(x+\sqrt{2-x^{2}})(x-\sqrt{2-x^2})}{\sqrt{2}})^{1/3}={(\sqrt{2} \cdot (x^{2}-1))}^{1/3}$
SirLancelotDuLac
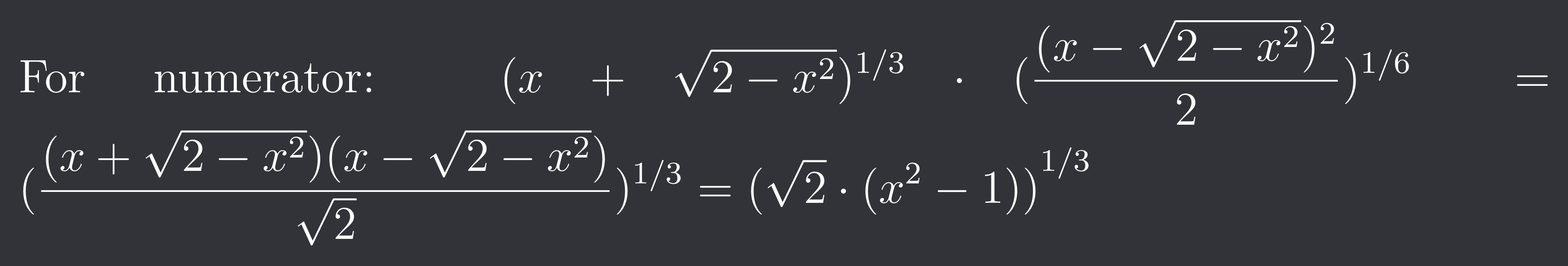
Okay I messed up the sign in the numerator
It should be 1-x^2 instead of its negative.
Anywho notice the numerator cancels the denominator giving a constant
@hardcoreisdead
@SirLancelotDuLac how do you write this sh..?
The "(edited)" says it all 😭
By hand???
How many hours does it takes?
Are it's code
It's a language called LaTeX
Which like types out that aesthetic math fontfor you
I mean you
$\frac{x^{8}+64+16x^{4}-16x^{4}}{x^{4}-4x^{2}+8}=\frac{(x^{4}+8)^{2}-(4x^{2}^{2})}{x^{4}-4x^{2}+8}=\frac{(x^{4}-4x^{2}+8)(x^{4}+4x^{2}+8)}{x^{4}-4x^{2}+8}=x^{4}+4x^{2}+8$
Raman
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)
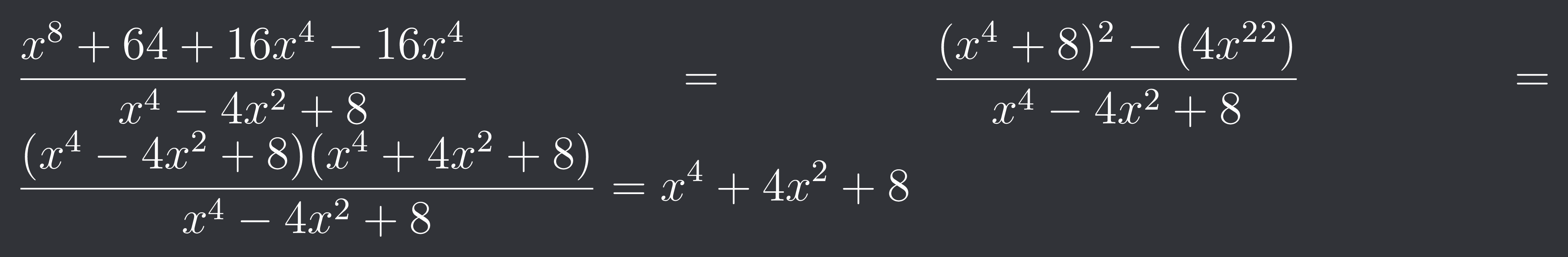
Write this
And it gives photo
So write code by hand
Its easy once you use it a lot.
Ok
So just need to go through hell once
@SirLancelotDuLac i solved it but the problem is i am getting a minus sign and given ans mein nahi hai
(hvnt read msgs above as of now)
i am getting -x*2^1/6
ans mein (-) nahi hai bas
how , 2x^2-2 hi toh aa rha. we'll take 2^1/3 out leaving us with 2^1/3 * (x^2-1)^1/3 in numerator
denominator is 2^1/6 * ( 1-x^2)^1/3
ab -2^1/6 bacha
Completing the square wale step mein galti kari hai ig.
Positive value actually mein sqrt(2-x²)-x hogi
eh will share my process in a few
Kyunki x 0 se 1 mein hai
yeh kisne kaha
oh han
damn
big brain ques
also how did u observe such an obnoxious thing
the conjugate ke sq wala part
@SirLancelotDuLac can u spot the error

Again the same thing. Note that it should be written as $\sqrt{2-x^{2}}-x$ and not its negative at all points.
SirLancelotDuLac

Because this is positive when x $\in$ (0,1)
SirLancelotDuLac

why do we need $\sqrt{2-x^{2}}-x$ to be positive
hardcoreisdead
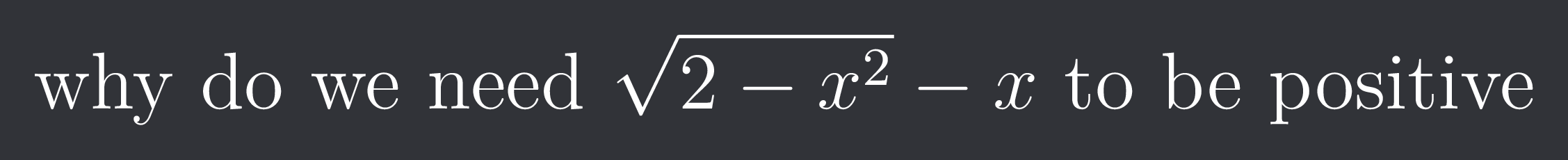
Lemme ask you this: What would be the value of $\sqrt{a^{2}-2ab+b^{2}}$?
SirLancelotDuLac
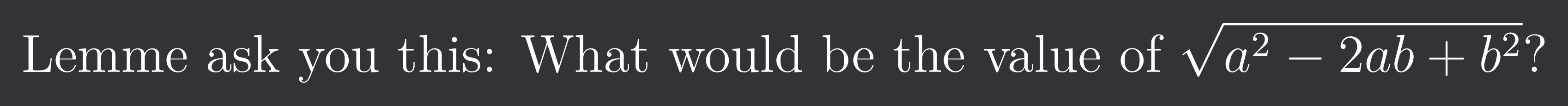
|a-b|
Ye exactly. The mod thingy. When we are converting the power 1/6 to 1/3, there is an implied mod. (Kyunki a^(1/even) is always positive while a^(1/3) may be any sign, get it?)
Which is ignored here.
ok so for x belongs to (0,1) , (x-(2-x^2)^1/2 is negative. since there is a mod , it will open with a -ve sign?

corret?
@SirLancelotDuLac
Yes.
got it
how do u even spot such things
1. the conjugate ka sq wala part
2. the mod part
1. When you have stuff like x+sqrt(c-x^2), its worth squaring to see what you get because x^2 and c-x^2 cancel the x^2 term and give you only a constt. and x.sqrt(c-x^2) term.
2. The mod part was because I noticed that the numerator I was getting above was cbrt(x^2-1) and denominator was cbrt(1-x^2) that gives a negative, but the expression in integral was always positive.
For x being in (0,1)
Oh wait, why would x be in (0,1) though?
x should be be (0,2)
T-T
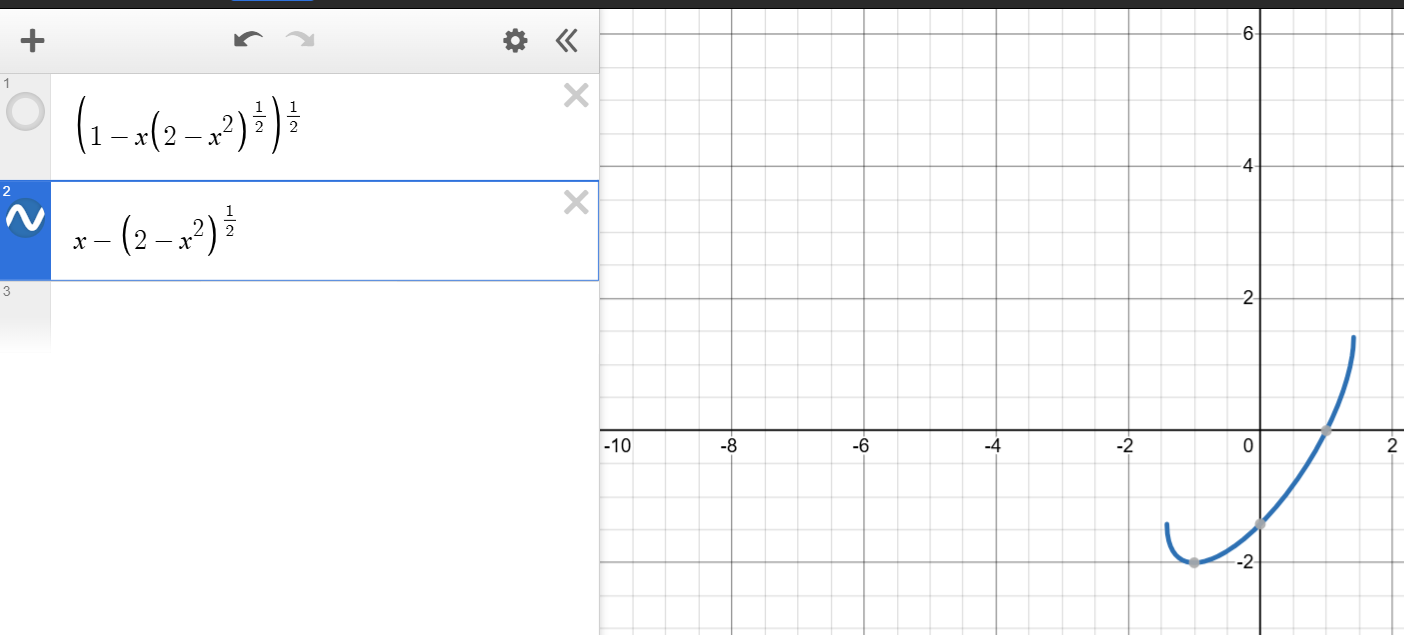
just when i thought i had it
But there is power 1/3 no?
Okay I overlooked this shi
Dayumm
I'll ponder over this tommorrow, too sleep deprived to function rn :psyduck:
theres a (2-x^2)^1/2 too
@SirLancelotDuLac i am closing this. will create a separate post for this particular ques
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1751994071:R>
Solved by
<@1075951732460376214> (1075951732460376214)