Integration
For ques 26 I took n=2 and the ans matched with key.
What's the proper way to get the ans

65 Replies
@Apu
,rotate
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.
@SirLancelotDuLac
One method is to wrote sin(n+1)x.sin^(n-1)x as sinnx.cosx.sin^(n-1)x+cosnx.sinⁿx
Then divide and multiply by n
You'll notice it forming as fg'+g'f
So it becomes sin(nx)sinⁿx/n+c
yeh kaunsi form hai ab
Chain rule na?
(fg)'=f'g+gf'
omg right
what made u think this
It seems reasonable to open sin(n+1) to sinnx and sinx and so on. Further it is helpful to think "What could have been differentiated to get an expression like this?"
You could also have done it easily with by parts, but I just wrote the first thing that came to mind lol.
Doing by parts is basically doing the above, 'cuz by parts is just inverse of chain rule
So both things are basically the same.
i am getting g(x) = (sinx)^n
f(x)= (sin(nx)*cosx)/n
i dont see f'(x) in the given expression tho
No, take sin(nx)/n as f(x) and sinⁿx as g(x)
sinnx.cosx.sin^(n-1)x+cosnx.sinⁿx
this term has g'(x) so the remaining portion must be f(x) right??
The first thingy has derivative of sinⁿx while the other has derivative of sin(nx)
oh right mixed up some terms
baaki bhi pls
Will look at them tommorrow :/
acha
bas ek cheez batado
for the first one in pic
numerator = k1 (denominator)+ k2(derivative of denominator) +k3
right?
i break it down like this
def k1 k2 terms rational de denge
problem lies in k3/(quad)^2
The lower one is not a whole square toh k1=0
by denominator i meant only the term inside square
(1/quadratic which is not a square) will not give rational function na.
Ye I understood that. But ☝️
arey han 1/( x^2 + a^2) type ka hoga
what should be the approach then
k2 works. As for k3 i gotta ponder over this. :/
this whole approach doesnt work tho right
ill have to think of another
Nah the approach seems correct.
abhi toh kaha 1/quad ka integration wont give rational
k1=0. Derivative of denominator will be linear. So we have an extra ax² term.
Ye so k1=0 na.
hain
ohh
nice question
Imma look at this tommorrow. :thinker:
jo ho bata do 🥀
free for all 😇
26th aise khud nhi dikhta 😔
25 batana ho toh
ill try 27 from your method
okk
From the above we deduced that k1 had to be zero yesterday. Following that train of thought, since the order of derivative of quadratic is 1, the term 'a' should be zero too. As remains b. Since the ratio of c and 2b is same as the ratio of 2B and 2A, we can say that c/2b=2B/2A.
And so we have our required answer
Ahhh we did like 90% of the question yesterday
@hardcoreisdead
how did u come up with c/2b= B/A
It must be k2.(derivative of the denominator) thingy
i did
2bx + c = k2(2Ax +2B) +k3
this gives b=Ak2 and c=2Bk2 + k3
can we proceed from here??
Oh right, I forgor about k3 💀
putting the obtained values in required ratio we get 2+ k3/Bk2
k2 is def non zero
k3/(quad which is not a square) can be written as c.k3.[1/(x-alpha)^2+1/(x-beta)^2-1/(x-alpha).(x-beta)]
The last term does not give us a rational term so it must be zero too.
$\frac{k_3}{(\alpha-\beta)^{2}}(\frac{1}{(x-\alpha)}-\frac{1}{x-\beta})^{2}$
SirLancelotDuLac
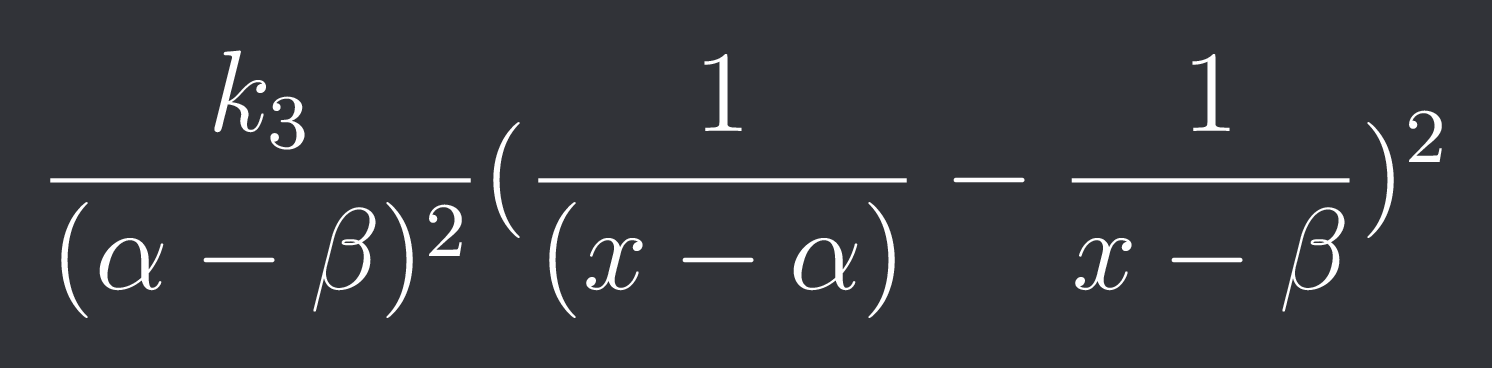
alpha beta are roots of quad ??
Yee
Even if they turn out to be imaginary, the results of rationality remain the same.
Because the log with imaginary stuff turns to arcsin or arctan by euler's theorem.
isnt it k3/(x-alpha)^2 (x-beta)^2
So we write it as the latex above though
When you'll open the bracket you get a term of type
$\frac{c}{(x-\alpha)(x-\beta)}$
SirLancelotDuLac
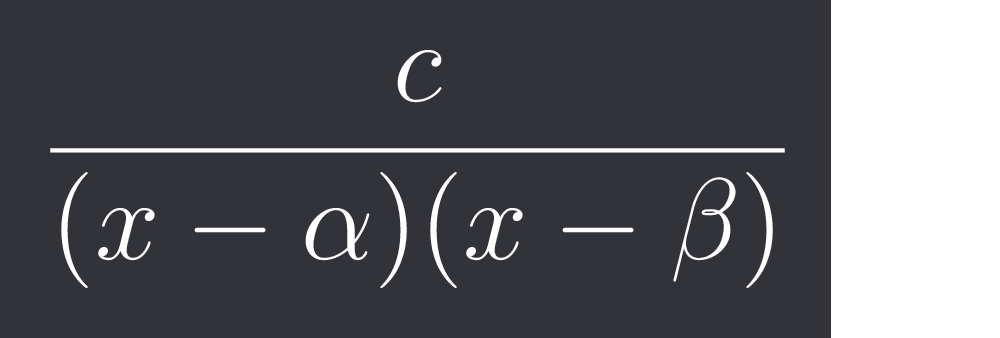
.
Yo @hardcoreisdead , you there?
processing
Ah, sorry.
ik integration of 1/quad doesnt give a rational function unless it has two real roots
right??
how can we be sure of 1/(quad)^2
As said above, you can split the quadratic inside to 2 1/linear thingies and then open the square to get something of the form c/(quadratic which is not a square)
*Unless its a perfect square
oh han otherwise it goes to ln()
instead of doing this can we write it using partial fractions
lets say it has real roots
so itll become of the form
P/(x-alpha) + Qx+R/(x-alpha)^2
similar for beta
now this doesnt give a rational function for sure
right??
Yeah.
Because of the Qx term
Which will try to turn the denominator linear
and also the ln
Oh wait no.
Yeah, but P/(x-alpha) term may cancel that ig :/
hmm
This makes it sure though imo.
That k3 must be zero.
hmm ig
i cam across another approach
since theres a ()^2 in denominator it mustve come from differentiation of u/v
u'v-v'u)/v^2 = given term
we let u =px^2 +qx+r
and then do some calcs to get relations
u should be linear though no?
Since we have quadratic in numerator.
oh yeah
But yeah, that could work.
even better
But what if the denominator here has degree 6 (i.e. v has degree 3) and the numerator has degree 4 (i.e. u is quadratic) and one of the factors just cancel out?
Oh wait nvm I'm dumb that's not possible.
Ye, it could work ig.
yep just did the calc
it checks out
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1752737075:R>
Solved by
<@1075951732460376214> (1075951732460376214)