17 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.$y^{2}=xy \cdot y'-x^{3}e^{\frac{y}{x}}$
Divide by $x^{2}$ on both sides $t^{2}=t \cdot y'-xe^{t}$
Now $t'=\frac{y'}{x}-\frac{y}{x^{2}} \rightarrow t'x+t=y'$
SirLancelotDuLac
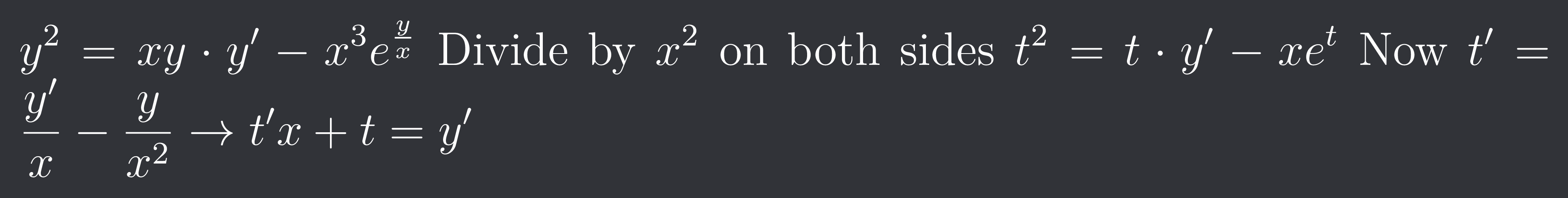


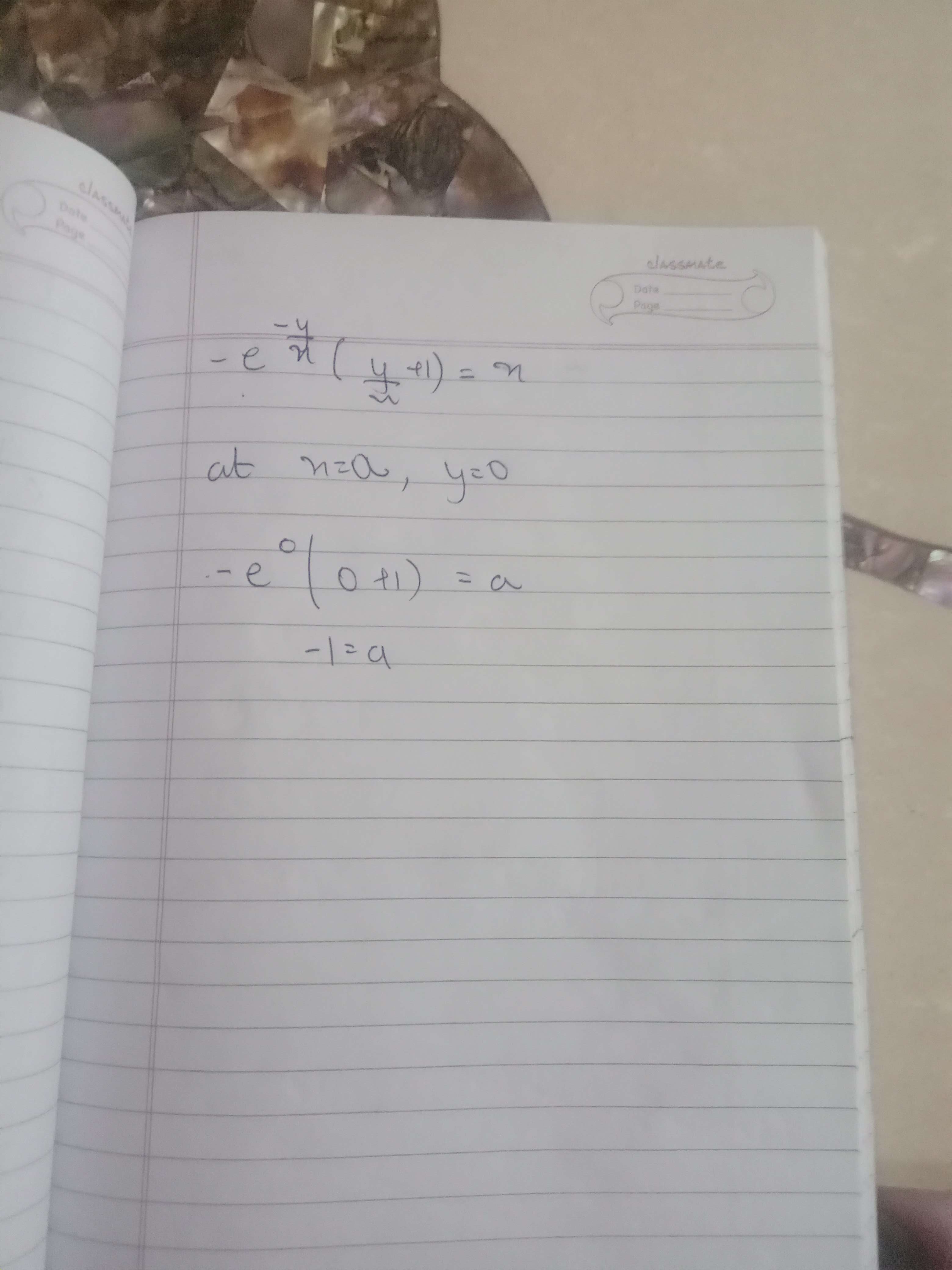
After this, $t^{2}=t.t'.x+t^{2}-xe^{t}$ which gives us $t.t'x=xe^{t}$ this, $t'=\frac{e^{t}}{t}$
SirLancelotDuLac

Or rather $e^{-t}.t.dt=dx$
SirLancelotDuLac
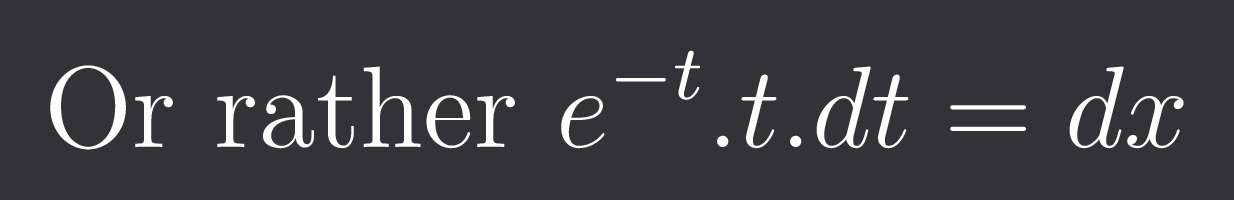
Just integrate that shi
@hardcoreisdead
Ans 0 ha kya?
whi toh kara hai
nope
Ye, so integrate karne pe e^{-t}(-t-1)+c
Since f(1)=1, x=e^{-t}(-t+1)+1
meine galat integration kia ha kya
can u check
Oh shit I forgot the x term on rhs
Since y=0, t=0.
Now x=e⁰(-0+1)+1 which
Is 2
Sowwy.
It is correct but you forgot the integration constant.
OMGG
😭
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1752855997:R>
Solved by
<@1075951732460376214> (1075951732460376214)