Limits diffrent method confirmation
The 2nd image is giving answer the 3rd one is giving 0 is it all correct?
Also how does a single limit have diffrent values?
Also how does a single limit have diffrent values?
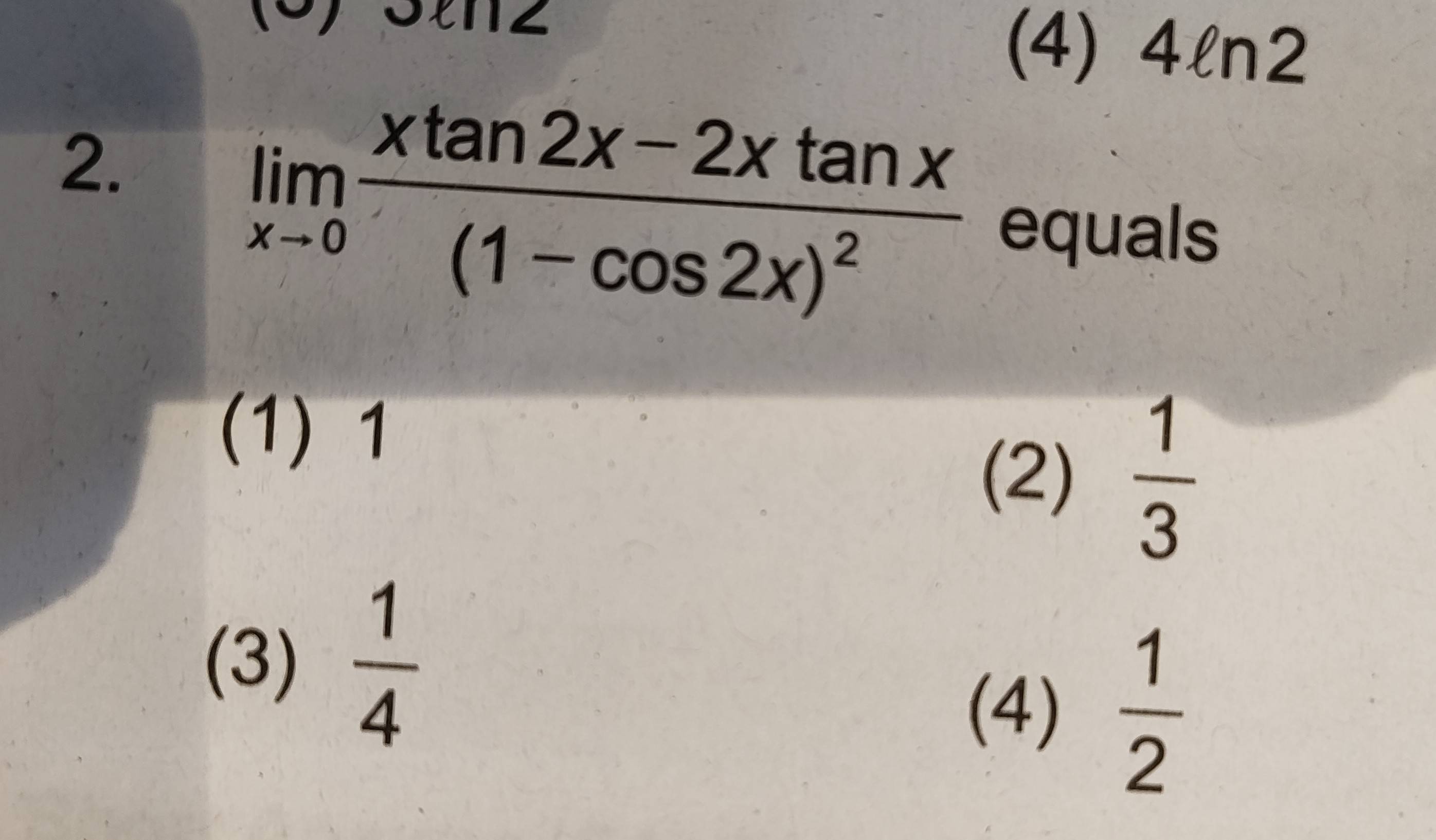


+solved @user1 @user2...discord.errors.DiscordServerError: 503 Service Unavailable (error code: 0): upstream connect error or disconnect/reset before headers. reset reason: overflow
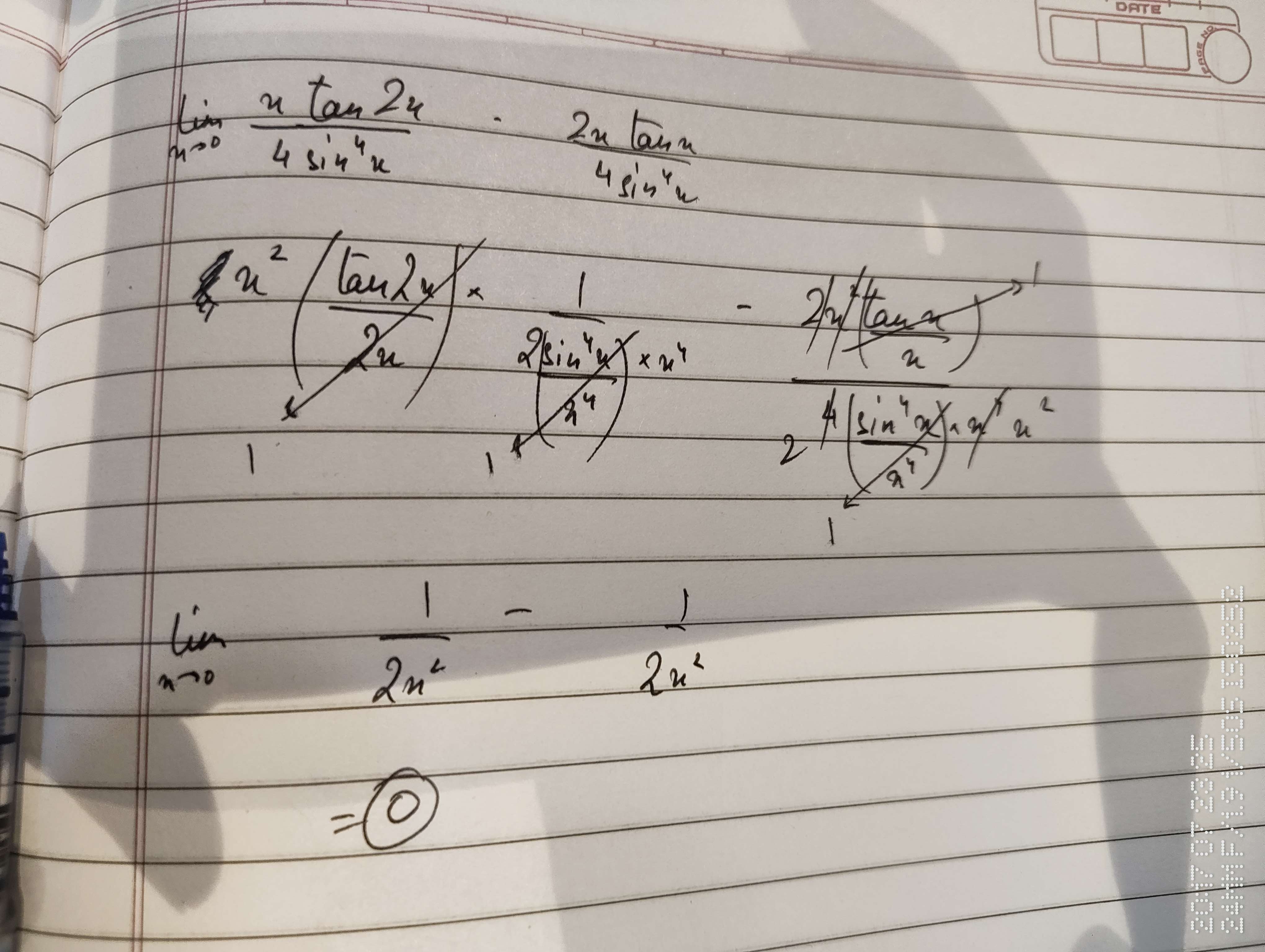
discord.errors.DiscordServerError: 503 Service Unavailable (error code: 0): upstream connect error or disconnect/reset before headers. reset reason: overflow