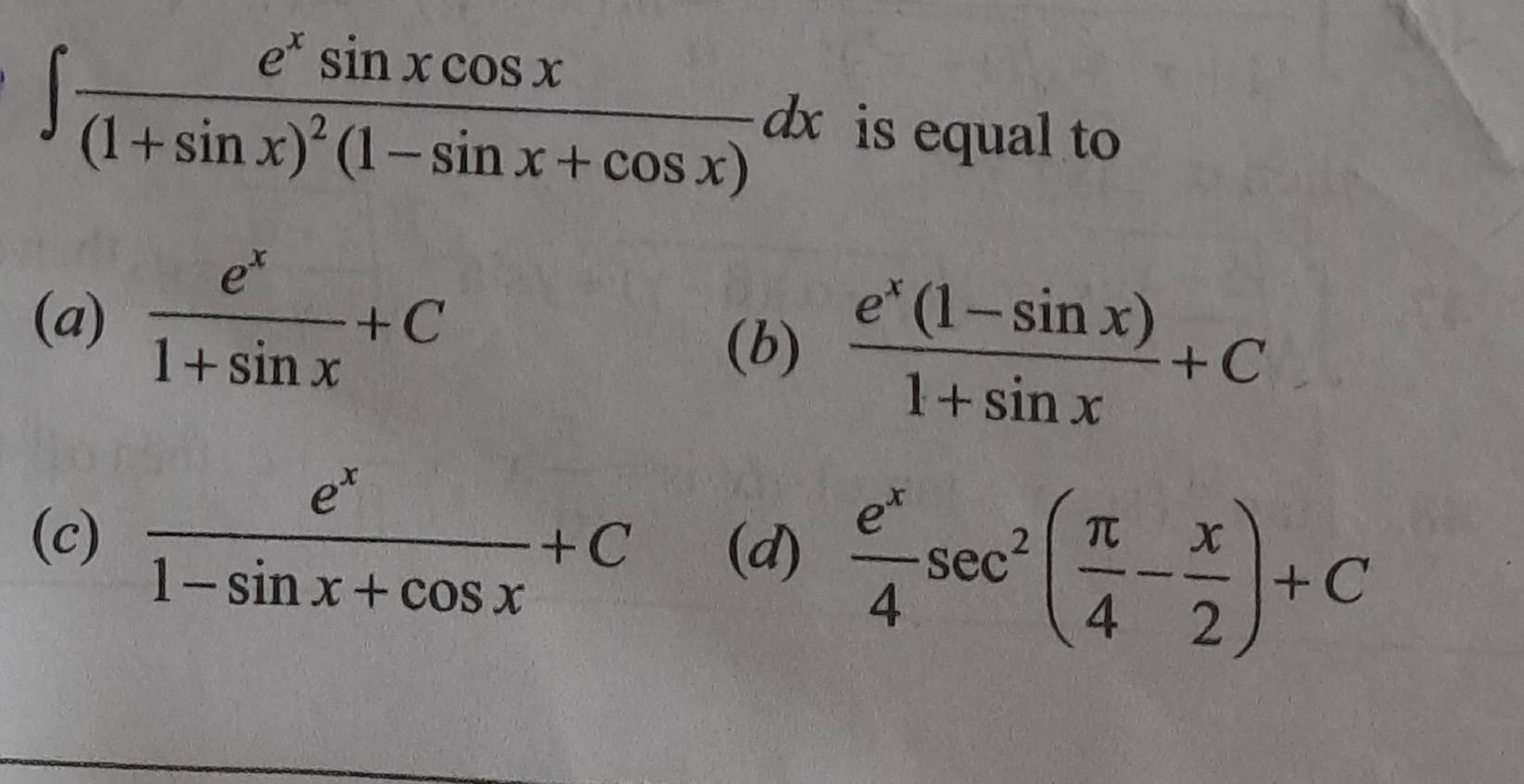9 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Ig sub x=pi/2-t
Kyunki then you'll be able to simplify (1+sin(x)) term and (1-sin(x)+cos(x)) term to half angles.
$\frac{e^{\frac{\pi}{2}-t}.sin(t)cos(t)}{4cos^{2}(t/2)(2sin^{2}(t/2)-2sin(t/2)cos(t/2)}$
SirLancelotDuLac
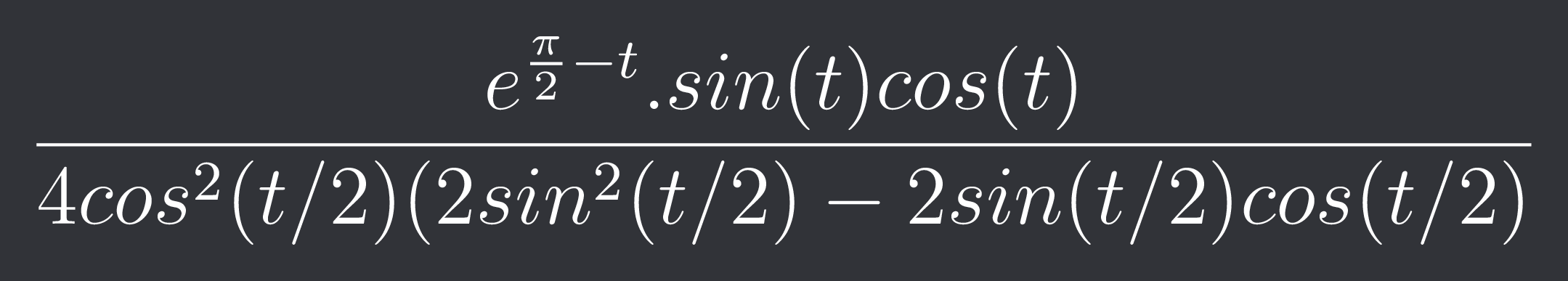
Write the numerator ka sin as 2sin(t/2)cos(t/2)
Some terms get cancelled and you get $\frac{e^{\frac{\pi}{2}-t}cos(t)sec^{2}(t/2)}{4(sin(t/2)-cos(t/2)}$
SirLancelotDuLac
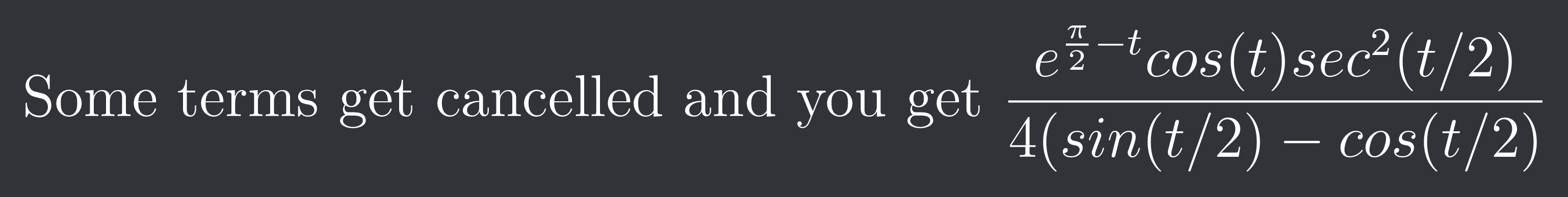
Write the denominator ka term as sqrt(2)sin(pi/4-t/2) and numerator mein cos(t)=2sin(pi/4-t/2)(cos(pi/4-t/2)
mai karta try isko
@SirLancelotDuLac
end mein kuch simplify hoke bach gaya
bhai humne thoda zyada soch lia
(sinx-cosx)^2 = 1-2sinxcosx
2sinxcosx = (1-sinx+cosx)(1+sinx-cosx)
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@1382187168230936577> (1382187168230936577)
Time
<t:1754334501:R>
Solved by
<@1075951732460376214> (1075951732460376214)