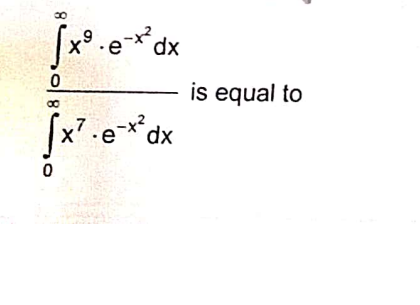70 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.will try tommorow, too sleepy rn.
bhai vo organic ke dekhlio yar 5-6 doubt khul rkhe abhi mere😭
will try
Sub -x²=t and then you get smth like ratios of integrals of e^t.t^n which is ratios of (n!)
i dont get how factorial comes in here
but i did what u said
and then did repeated byparts
to get integrals
this
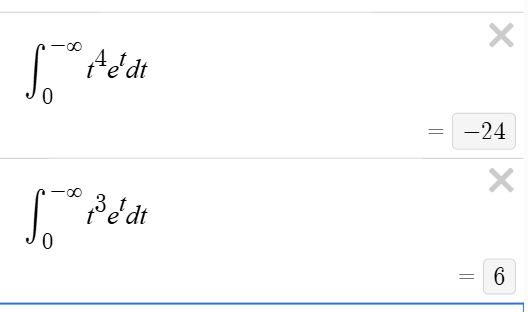
the ratio is somehow -4 tho
-x^2=t
since x goes from 0 to infinity , t goes from 0 to -infinity
Because x² changes to -t and not t. So oowers of form 4k+1 get changed to t to the 2k while those of form 4k+3 get changed to -t to the 2k-1
Search up gamma function. (Not jee relevant but for natural numbers you can see how the result comes up.)
(Also I thought this was in Aakash Modules so...)
literally msged this to u in dms 💀
what?
-x^2=t
-2xdx = dt
x^9 e^-x^2 dx = t^4 e^t dt/2
i just simply did this
@SirLancelotDuLac
First of all sorry, we would have to take x²=t and not the negative. (Sorry)
After this, as mentioned above, the integral ratio is equal to ratio of factorials, which gives rhe answer 4.
Ill look at your approach later but the method i posted above doesn't work
Why
I think you messed up signs as said above
Imma write it out and send in the evening.
doesnt make much diff . ratio hai kat jayega
Nah note that -x² ko t liya hai
Toh x⁶ us -t³
whi realize hua abhi
Not t³
Holy crap the heat melted my brain 😭
tripura heat is 🔥
*Tirupati 😭
same shit 🔥
btw
i still dk
beta and gamma function kitna aur kahan se karu
(module mei nahi hai)
Bro I thought all aakash modules were supposed to be same but...
Wait can you find pirated?
Just for Def. Int?
'Cuz the way stuff is there makes it soo much easier
Is ques 10 somewhere related to them??

invictus 🔥
Nah 10 is doing byparts na.
Oh sorry that's 9 lol
9 is wallis theorem??
Yup. So is 10 if you sub x=cos² ig?
Actually you can do this is beta and gamma functions but....ehh
wallis theorem mei factorial kahans e aagye
Don't do it too rigorously but yea
You can watch videos and shi
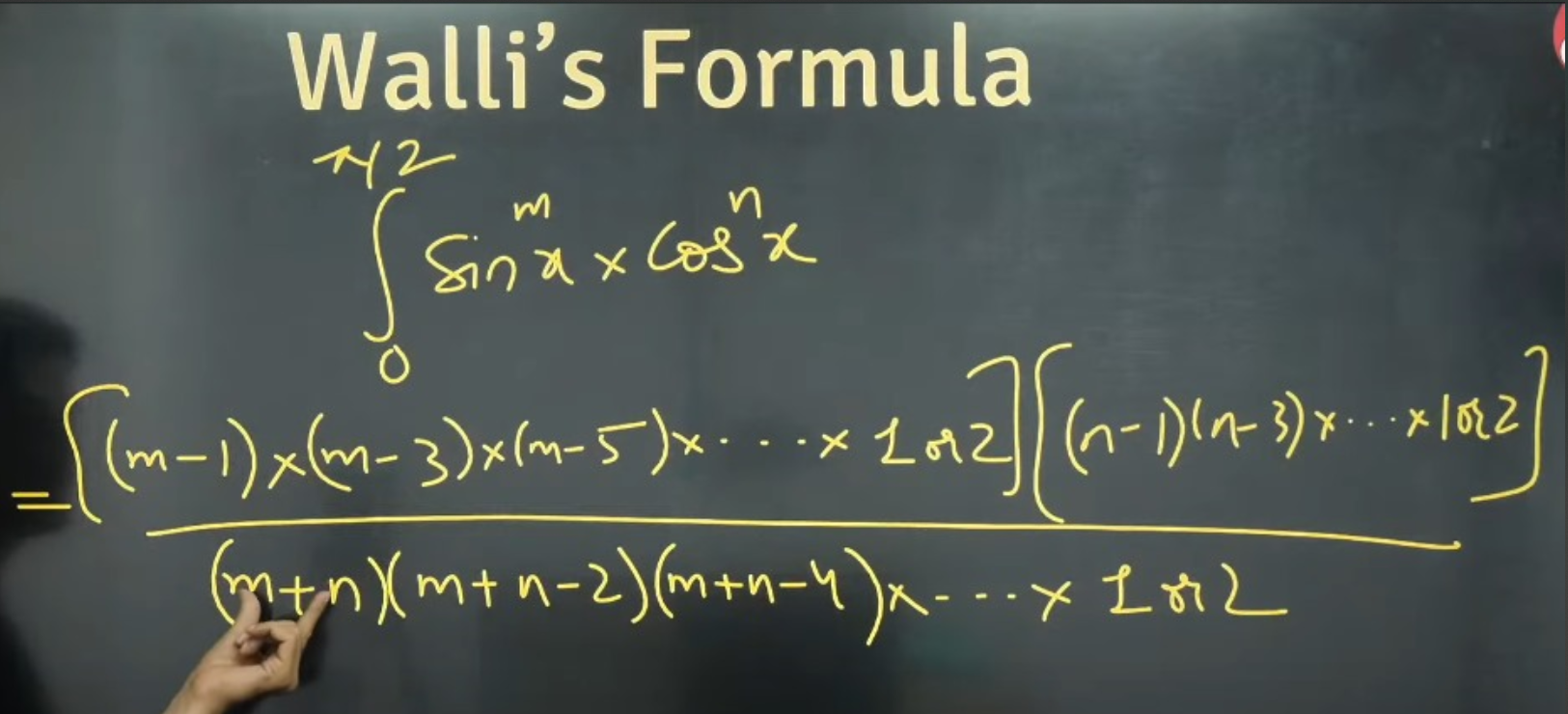
thing is extra topic hai
so theres no bounds
There is another form for that. One involving gamma functions.
Just the very very basics.
Only the algebraic stuff ig.
Wait Imma try and find that stuff... :/
:sweaty:
do u have all the relevant stuff in your notes or smthing
@SirLancelotDuLac updates??
Ye man, I don't have any pirated copies of aakash modules 😭
Ig you could ask in jeeneetards server.
If the resources channel is still there
OH WAIT
,rotate
Couldn't find an attached image in the last 10 messages.

,rotate
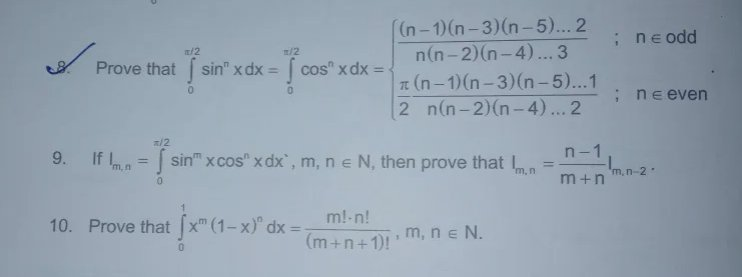
@SirLancelotDuLac how is 9th walis formula
shouldnt it have (m-1)(m-3)(m-5)..... too
and 10th is just beta (m+1,n+1) ??
how tf is wallis formula different everywhere
kahin pi/2 ha kahin nahi

ig this variation is wrong

this correct
wtf is 9th then
also yeh jo beta gamma function hai what does using (bx-a) give
@SirLancelotDuLac pls online 🙏
Oh sowwy forgor to respond 💀
Hmm...you can change it via substitution to the x^p(1-x)^q form though ig?
Gamma function🗿
huh
e^ kahn gya
nvm though i got it
clear the wallis formula confusion
@SirLancelotDuLac
coaching slop
@SirLancelotDuLac
Wait Imma write it on paper and send
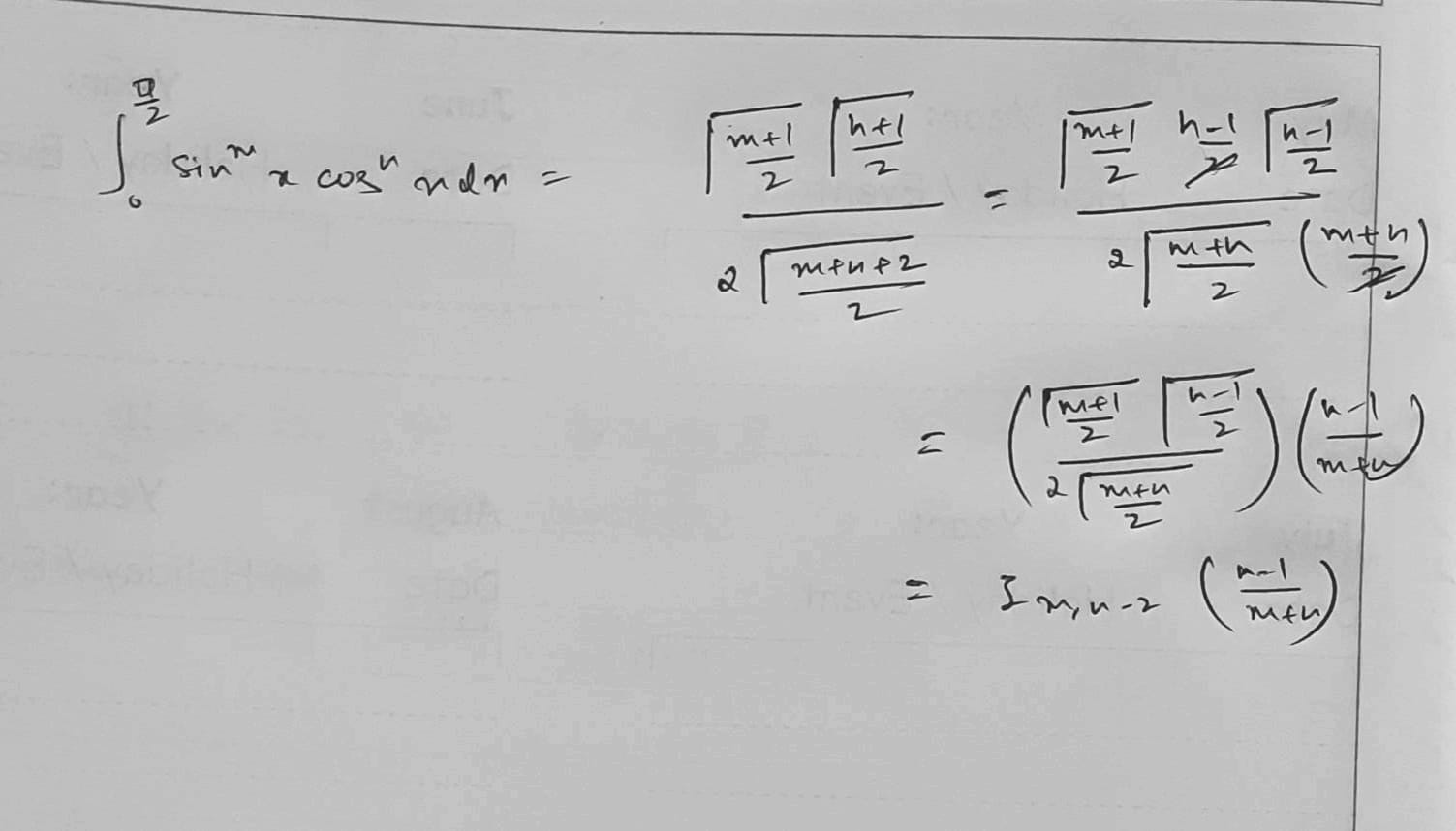
this form is wrong then ....
and this correct
This is correct but there are a lot of cases and shi to remember in the image one. If you use gamma function wala thingy and you know gamma of 1/2 is sqrt(pi) it simplifies stuff out.
I used to suck at remembering cases so this was gold for me. 🙏
what if i get gamma (5/2) thing
gamma(n)=(n-1)gamma(n-1)
gamma(5/2 ) = 3/2* rootpi
Since walli's formulae ke gamma wale form se (stuff)/2 wale terms aate hai either you get straight up gamma(integer) which is (integer-1)!
Or you get (odd integer/2) which can be simplified
odd mein hi dikkat thi
3/2.gamma(3/2)=3/2.1/2.gamma(1/2)=3/4*sqrt(pi)
ohh
Baaki you can remember cases also
here n-1 >0 i.e n>1 riht
right
Techinically the gamma function diverges at only negative integers, so you could in fact have gamma of (-0.5)
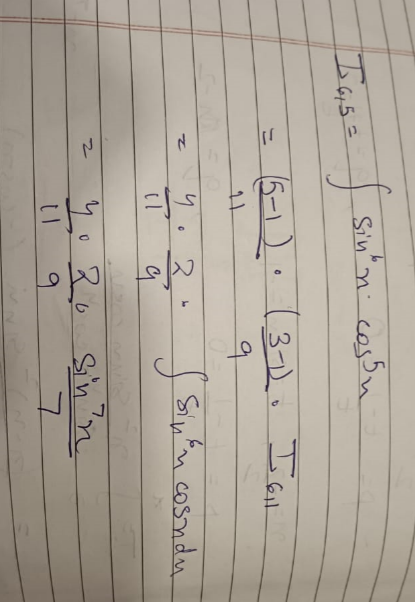
Otherwise ye, here the value of gamma ke andar wali cheez should be +ve here
For evaluation purposes.
what bout this
puting x=pi/2 we get 8/11* 63
Ye, this is from 9th only na?
ok yes same hai
gamma(7/2).gamma(3)/2.gamma(13/2) which is (5/2.3/2.1/2.sqrt(pi))*2!/11/2.9/2.7/2.5/2.3/2.1/2.sqrt(pi)
Which simplifies to the above
If you wanted it done by the gamma function thingy.
alrr
that summarizes it ig
will close this once i write it down in my reg
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1755009890:R>
Solved by
<@1075951732460376214> (1075951732460376214)