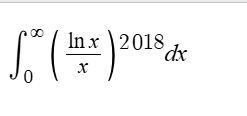29 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.i thought of taking lnx = t so x = e^t . then doing repeated byparts
however every term just becomes zero
lnx=t then, $e^{-2018t} \cdot t^{2018}$ from 0 to infinity and then remember that gamma function thing I told you about?
SirLancelotDuLac
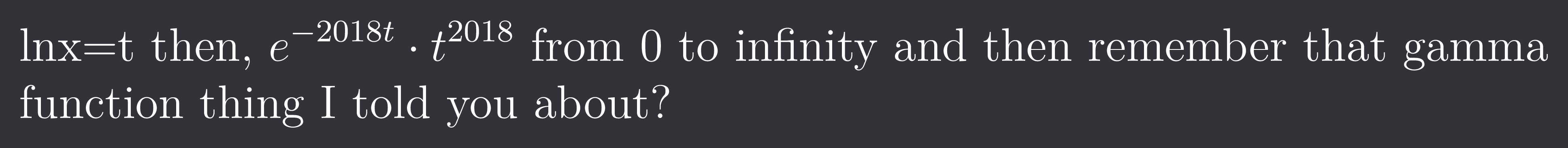
holy shit
wow
$\int_{0}^{\infty} e^{-2018t} \frac{(2018t)^{2018}}{2018^{2018}} \cdot dx=\frac{2018!}{2018^{2019}}$ ig?
gamma funciton for the win
2017^2019
SirLancelotDuLac
one 1/x will be used up to convert dx to dt

@SirLancelotDuLac small doubt so adding in this only
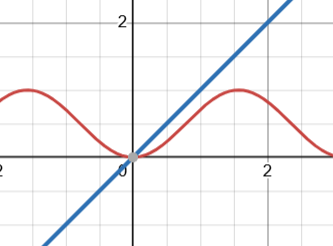
f(x)=1-cosx = 2sin^2x
how do i approximate the values in column 1
and column 3
Ooh right, I'm sleep deprived.
Wait on that thought, Imma get some tea and come back. ;_;
lol alr
can i replace sin^2x with x
seems close enough
Differentiate both sides and simplify to get $f''=\sqrt{1-(f')^{2}} \rightarrow \frac{df'}{\sqrt{1-(f')^{2}}}=dx$ and get f' from there
SirLancelotDuLac

Which turns out to be sin(x+c) ig
(for x being in 0,pi/2)
And after that, f is then just -cos(x+c)+d
f'(0) is zero so c=0
And f(0)=0 so d=1
Then you get f as $2sin^{2}(\frac{x}{2})$
SirLancelotDuLac
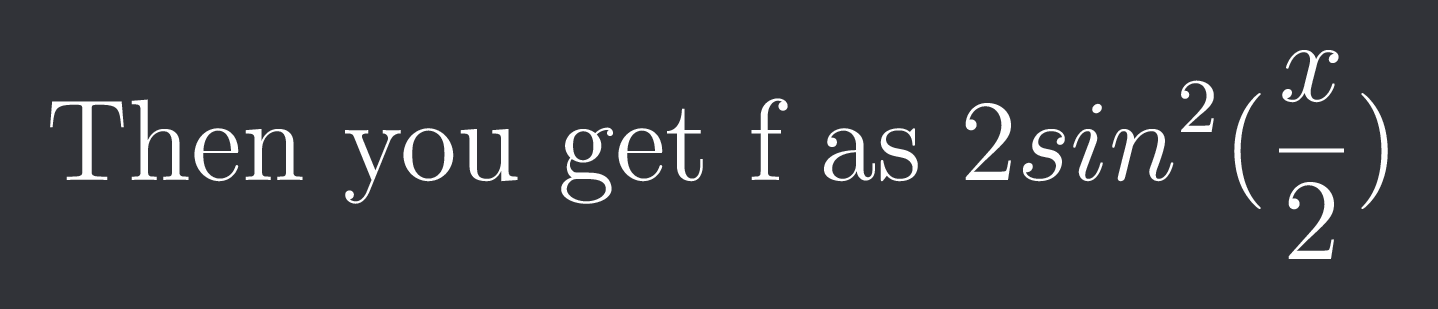
i took sinx + c T-T
f(x) still comes out to be the same lol
yeh toh aa hi gya tha
its about approximation
Ah mb. Then approx it as x^2/2 na?
yeh kaise socha
sin(x) tends to x as x tends to zero wala concept.
x^2/4 hua na fir
(But do note x^2/2 is greater than our expression here)
Mhm. 2*(x^2/4).
overall yes
itna idea kaise lagta hai
x>sin(x) for x>0 wala concept.
(You can also plot in desmos ig to get a clearer visualization)
For the third column the integration would be smth like 1+sin(1). Since sin(1)>0, integral>1
why not just integrate x^2/2 and compare
column 1 se 1,3,4
column 2 se 3
column 3 se R and S
yhi shi aa rhe
aa gya sab
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1755965075:R>
Solved by
<@1075951732460376214> (1075951732460376214)