20 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Am gm laga k try kia lekin usse kuch ban hi nhi raha aisa ;-;
$$2^{2n+1}>1+(2n+1)2^{n}$$
Real potato
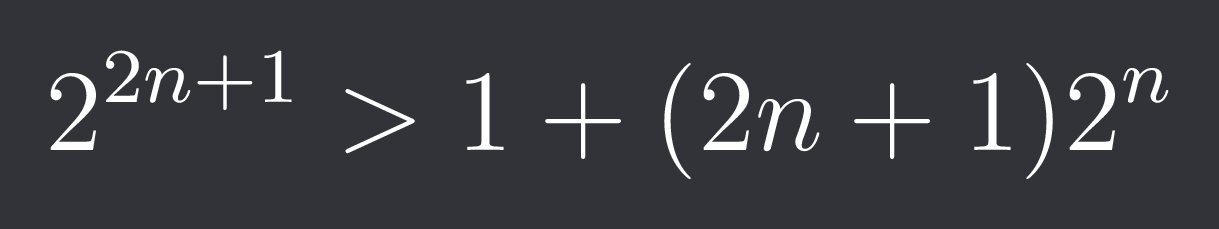
Mathematical Induction OP for these things
Ah i see.. i dont know anything about abt that chapter lol
The question said "n is an integer" that's why I suggested that.
Just do differentiation or smth.
SirLancelotDuLac
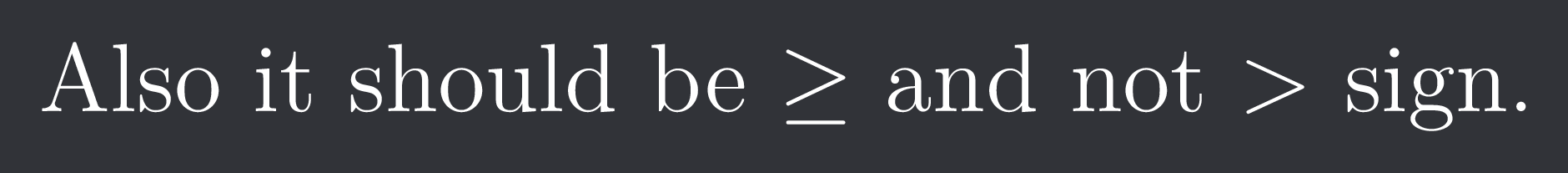
Ah nvm it says positive integers.
Show function 2^(2x+1)-1-(2x+1).2^x is monotonous and then f(0)=0
So we're done.
Lol was it that easy.. i was thinking of it as some sort of series and finding general term cause i found this plm in my sns notebook
Yea you can do it that way too.
i cant see any series here ;-;
Yea, I'll do this by sns and send the answer (if possible, I don't have paper on me rn)
sure !! No hurry
thanks
Agar sns se solve ho gaya toh कृप्या mujhe bhi ping kar dena
This looks interesting
yo lance any updates on this?
Couldn't do it by series, but one way I approached it initially was derivatives.
$\frac{2^{2n+1}-1}{2n+1}>2^{n}$
SirLancelotDuLac
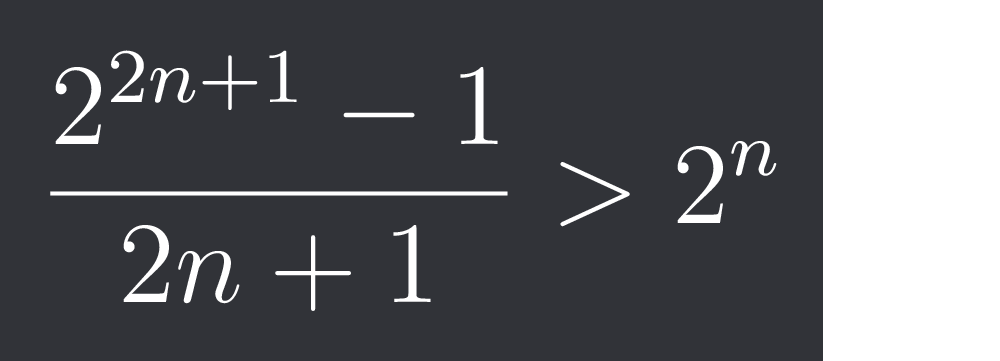
This is the slope of secant from 0 to (2n+1).
@Real potato @SirLancelotDuLac
If we say F(x) = 2^n
From graph, as you mentioned the slope of secant, since the function 2^n is strictly increasing, the functional value will always be less than the average value of slope in the interval (0,2n+1).
What I mean to say is,
(F(2n+1) - F(0))/(2n+1-0) > F(x), where x belongs to (0,2n+1)
Therefore, 2^(2n+1) - 1/2n+1 > 2^n
It's more of a calculus question?
Although there could be some method with SNS