Funct
Que-2
I have analysed the function and realised that the values are repeating and soi found a value for f(2000) but im getting 5/6 ans is -6/5

32 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Smthg like this
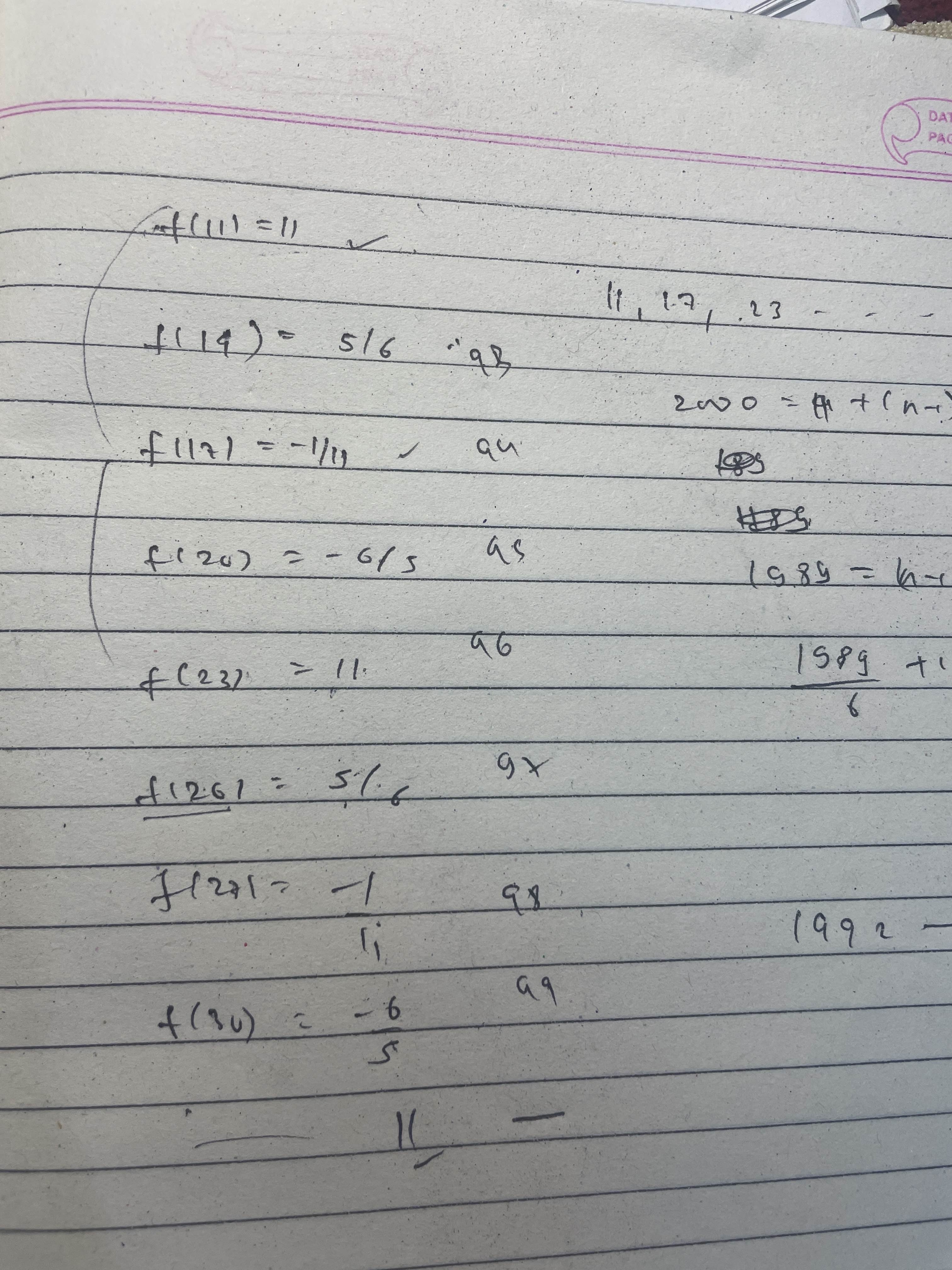
,rotate
💔
@Real potato Can you rotate this?
.
Oh u want the que
Wait wait

Yeah I seem to get the same
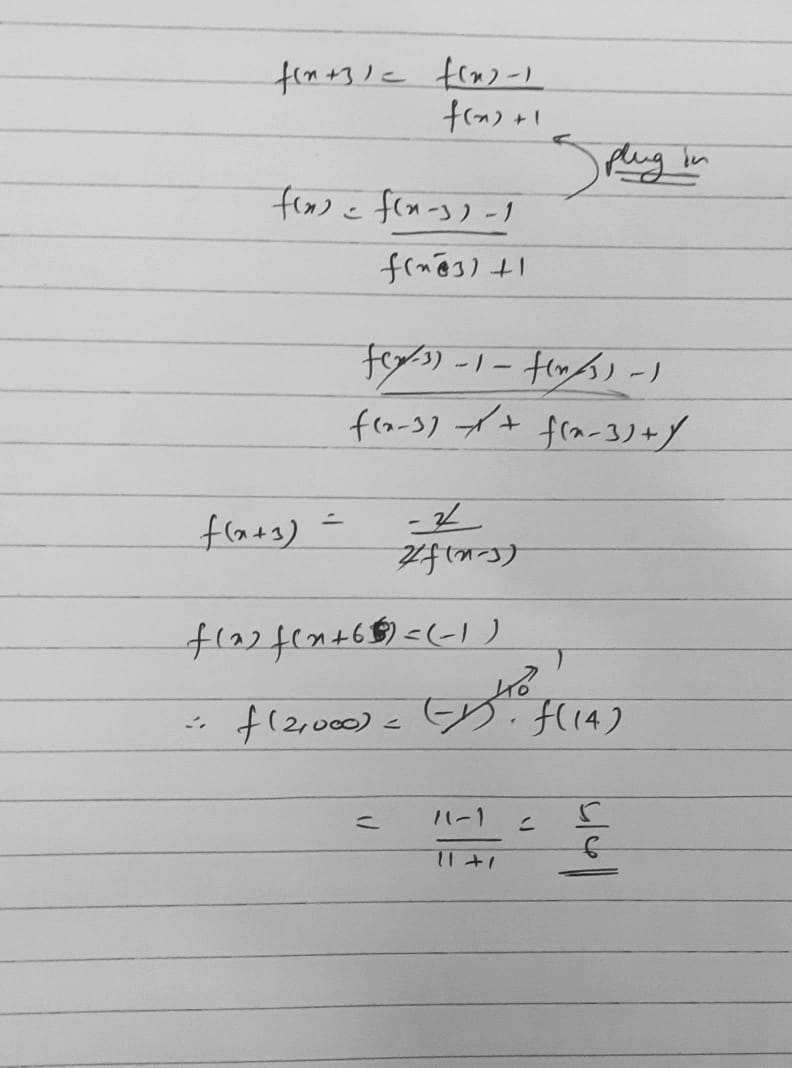
But the key says -6/5 ;-;
Nah I think the key is wrong :/
How did my teacher convince me that the ans is -6/5 only
:kekw: ill get it checked once
Can you look at que 1 too?
I'll check this once too then lol
aight
Notice that f(x)+f(1-x)=1.
Yeahh
I got the rest
W observation
Toh uske baad write sum as (f(1/2006)+f(2005/2006))+(f(2/2006)+f(2004/2006))....
Oh lol
how did you figure out this?
This question is asked a lot 😭
I hve been trying this que from 20 minutes :aah:
Anyways thanks a lot lancelot
Ill close this out once i clear that 5/6 one
f(x) = f(x+12)
Periodic fn
therefore, f(2003) = f(11) = 11.
Ans = -6/5
@Real potato
a^x/(a^x + a½) is a general format
f(x) + f(1-x) = 1 always
The ans given in key is correct
2005/2 is ans
Can you explain that ?
Replace x with x-3 and apply componendo dividendo to find f(x-3) in terms of f(x)
Then you will get a relation between f(x+3) and f(x-3) by eliminating f(x)
The relation is: f(x+3)f(x-3) = -2
Now replace x with (x + 6) and divide the both equations
You get f(x-3) = f(x+9) or f(x) = f(x+12)
I think there could be an easier method to find the period
But that's what clicked me the first time
I know its periodic you could easily find 4-5 values and see
But the thing is im not getting f(2000) as -6/5
I see
can you write up the soln on a paper if possible?
Alright
@Real potato

I found the term of the ap that is closest to 2000, it turned out to be 2003
It is -1 not -2
.
Yeah mistake