16 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.no idea tbh
idts second eqn is becoming of the form distance of point from fixed line=distance from fixed point
im thinking
triangle inequality
so perpendicular
wait lemme try
yeah so
say we make a new point
P
which has coordinates (-1,-1)
so just a reflection of A in the x-axis
the shortest path distance will be when you have P, the point on the x axis and the point on the parabola on a straight line
makes sense intuitively too but you can see that triangle inequality se
so you have to find the shortest distance parabola ka from (-1,-1)
bas reflection wala part samajh nahi aaya
and how did u integrate triangle inequalities in this
so
wait lemme desmos this for you
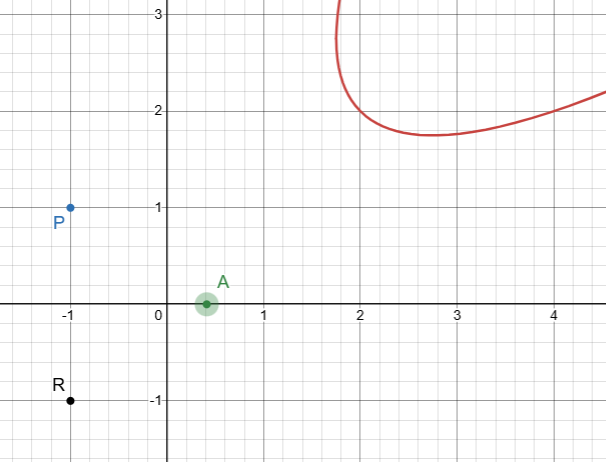
We are asked to minimize |PA| + |AC| for some point C on the parabola. Essentially, you have to minimize the distances PA and AC. For a moment, consider the reflection of the point P in the x-axis, say R. It is at the same distance from any point on the x-axis and thus PA=RA. But the key is that |RA| + |AC| is a lot easier to compute and can be done with a simple diagram which will tell you that the shortest distance (issi mein triangle inequality lagali thi but you don't need it) is going to be when R, A, C are collinear. In that case, you can simply remove A from the problem and simplify it to finding the shortest distance of (-1,-1) from the parabola.
sorry i forgot to mark C
but parabola pe hai
ohhh okay got it
nice solution
thanks
haan
waise
ek question kara hua hai maine aise
aisa*
ruk sending
its easier than this
but based on the same thing
iirc hume st lines me bhi aise karae the just not the parabola part
A man starts from the point P(-3, 4) and reaches point Q(0, 1) touching the x-axis at R such that PR + RQ is minimum. Find the point R
well just have to find the eqn of line from -3,-4 to 0,1 right?
yes
hmm ok got it
+solved @professional_procrastinator
Post locked and archived successfully!
Archived by
<@1336740240563372134> (1336740240563372134)
Time
<t:1763099461:R>
Solved by
<@737894194902990878> (737894194902990878)