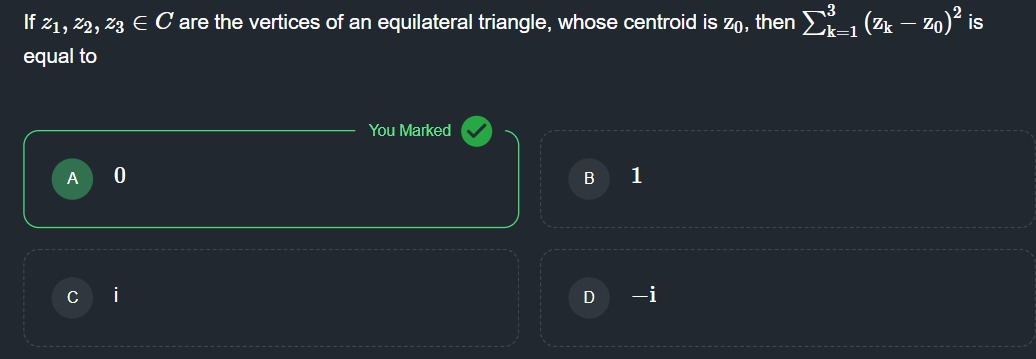
complex no.s
i got it by the normal method of identities in eq triangle thing in complex numbers. but can we do this by taking a complex number as a vector?
5 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Wlog take z0 to be the origin.
Wlog we can write each of z1, z2, z3 as the third roots of unity multiplied by a complex phase.
Taking the complex phase (squared) out of the summation, you end up with sum of the three third roots of unity which is zero
hmm i am getting answer by this method
got it thanks
+solved @Opt
Post locked and archived successfully!
Archived by
<@1336740240563372134> (1336740240563372134)
Time
<t:1764132140:R>
Solved by
<@763645886500175892> (763645886500175892)