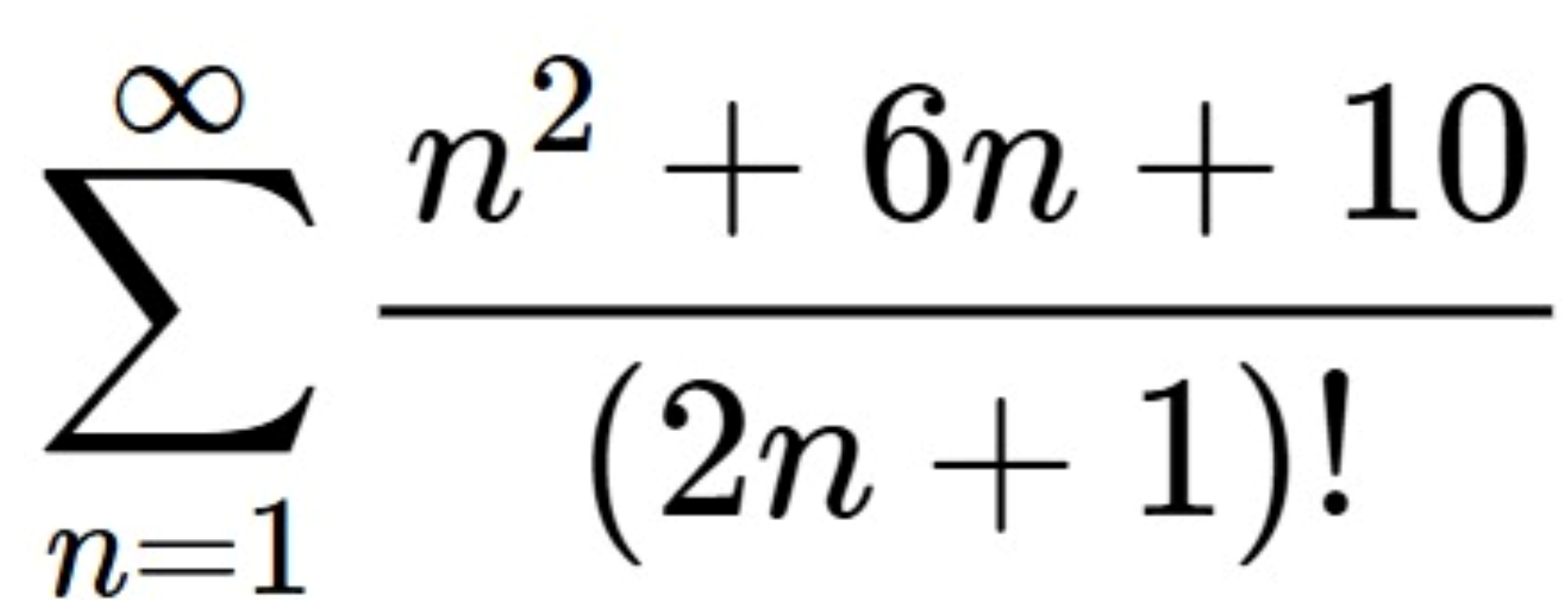19 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Ayo
Okay one approach can be this: Consider taylor expansions of $\frac{-e^{-x}+e^{x}}{2}$, where we have $\sum_{n=0}^{\infty} \frac{x^{2n+1}}{(2n+1)!}
Lance who?
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)

Now replace x with $\sqrt{x}$, to get the taylor expansion as $\sqrt{x} \cdot \sum_{n=0}^{\infty} \frac{x^{n}}{(2n+1)!}$
Also replace it on the lhs
Lance who?

Uske baad do the differentiation thingy to get the answer
Thoda brute force ahh thing hai but ye...:/
(Also forgot to write: This might turn out to be easier as the numerator thingy is effectively (n+3)^2+1, sooo yee)
ok so i watched a vid on this and the soln was really but kinda hard to think of
didnt involve differentiation
i am not sure if your method will work
It should tbh
Also yea differentiation is really cool for solving such problems 'cuz yk the taylor expansions
could you send it here?

now use taylor series



nice
+solved @AY @Lance who?
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1764704022:R>
Solved by
<@928940800178544691> (928940800178544691), <@1075951732460376214> (1075951732460376214)