Token count as in context window? qwen1.5-7b-chat-awq can handle a context of ~20k tokens, qwen1.5-14b-chat-awq ~7.5k, and llama-3-8b-instruct-awq ~8k. (Based on my testing.) Those are also limits for the total number of tokens, including output.
Hmm.. interesting..
@cf/mistral/mistral-7b-instruct-v0.2-lora has a context (and total limit) of ~15k tokens and you don't need a LoRA to run it.huh i tried to pass number array as image to dreamshaper
but got the error
Hey folks,
I am getting authentication errors when using the workers AI, the curl and python requests that is auto generated also is failing.
{'success': False, 'errors': [{'code': 10000, 'message': 'Authentication error'}]}
I am getting authentication errors when using the workers AI, the curl and python requests that is auto generated also is failing.
{'success': False, 'errors': [{'code': 10000, 'message': 'Authentication error'}]}
@cf/lykon/dreamshaper-8-lcmdoesn't support passing an image. try @cf/runwayml/stable-diffusion-v1-5-img2img if you want to do image-to-image.API call to the cf: https://developers.cloudflare.com/api/operations/workers-ai-search-model
If you care about custom upload loras: https://developers.cloudflare.com/api/operations/workers-ai-list-finetunes
public loras: https://developers.cloudflare.com/api/operations/workers-ai-list-public-finetunes
If you care about custom upload loras: https://developers.cloudflare.com/api/operations/workers-ai-list-finetunes
public loras: https://developers.cloudflare.com/api/operations/workers-ai-list-public-finetunes
Interact with Cloudflare's products and services via the Cloudflare API
Interact with Cloudflare's products and services via the Cloudflare API
Interact with Cloudflare's products and services via the Cloudflare API
You could also turn it into a ci build step that runs on a schedule and include it in your release
I did it here in GA in bash: https://github.com/demosjarco/matt-ai/blob/production/.github/workflows/ai-catalog.yml
End result (json): https://github.com/demosjarco/matt-ai/blob/production/shared/workers-ai-catalog.json
End result (ts): https://github.com/demosjarco/matt-ai/blob/production/shared/workers-ai-catalog.ts
I did it here in GA in bash: https://github.com/demosjarco/matt-ai/blob/production/.github/workflows/ai-catalog.yml
End result (json): https://github.com/demosjarco/matt-ai/blob/production/shared/workers-ai-catalog.json
End result (ts): https://github.com/demosjarco/matt-ai/blob/production/shared/workers-ai-catalog.ts
GitHub
Magically All The Things AI. Contribute to demosjarco/matt-ai development by creating an account on GitHub.

GitHub
Magically All The Things AI. Contribute to demosjarco/matt-ai development by creating an account on GitHub.

GitHub
Magically All The Things AI. Contribute to demosjarco/matt-ai development by creating an account on GitHub.

@Perry Sahnow because these count towards the global rate limit (1200/5m - https://developers.cloudflare.com/fundamentals/api/reference/limits/), you could cache the api results or go the build step method
I personally have mine set to update weekly and just watch and see how big of a commit (if any) happens in a given week - adjust from there. I did ask michelle about scheduled update cycle of models going forward, but they don't have any planned yet
huh i think the ai isn't recognizing my tools?
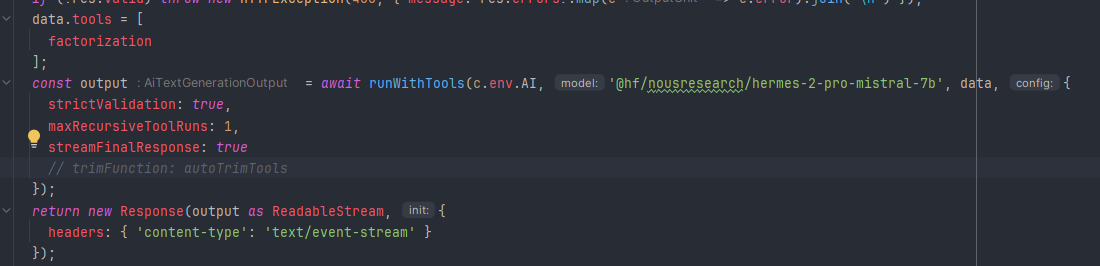
the function is not being called at all
didn't work even if i change the type of number to "number"
nvm i got it fixed
Can this be done from durable objects?
News for multilingual embedding model ?
qq; is there a limit on the response length from the LLM?
And, a "less quick" question
Is there a way to do a
Specifically trying to get an LLM to take an input like "dogs" with a system message of "generate a trivia question based on the topic and respond in json format of
Do the worker ai response is )
)
Is there a way to do a
json_format response with workers AI? (like what OpenAI supports) Specifically trying to get an LLM to take an input like "dogs" with a system message of "generate a trivia question based on the topic and respond in json format of
{ question: "string", answer: "string" }Do the worker ai response is
{question: "what is the best dog", answer: "all of them"} (made this up  )
)Ya each model has diff max token output
BAAI/bge-m3 is ok, from the same family of the already supported
Why didn’t Workers AI Playground work?
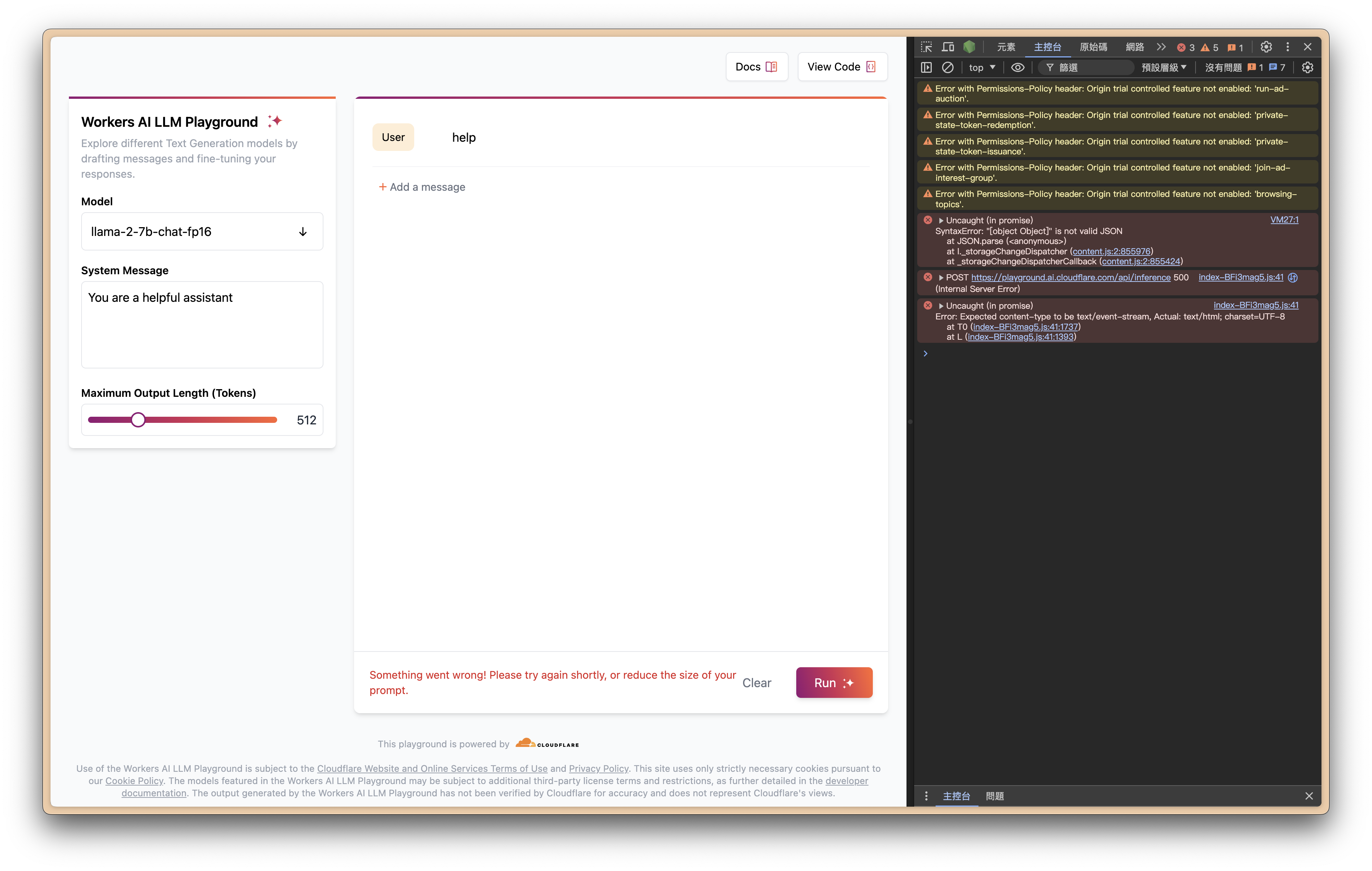
homepage demo is also broken
did you also see my video
here
maybe related issues?
but
sweet, I was finna say "its still not working" but nice ninja edit and nice quick fix!
I logged all data I had received from a streaming Workers AI call and got a key called
p. What is that?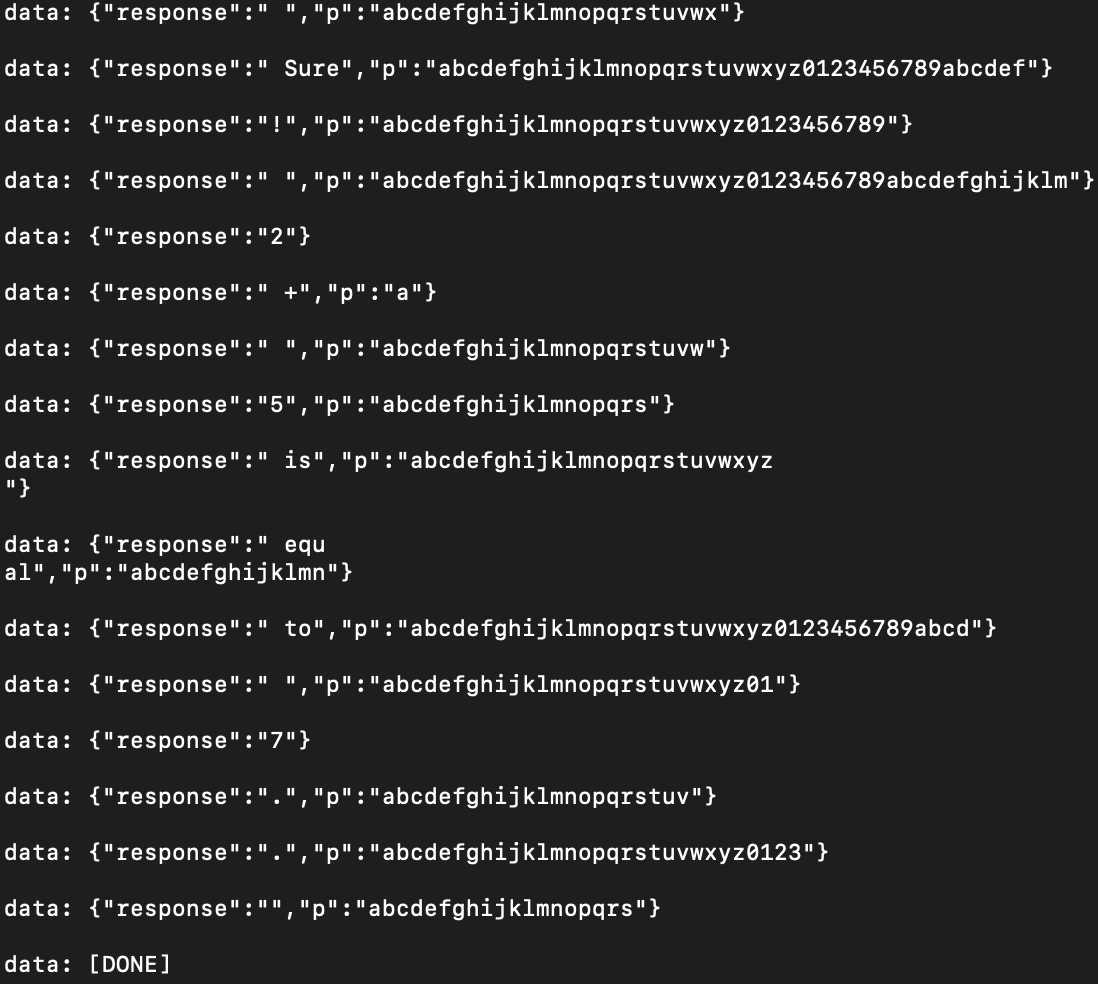
The Cloudflare Blog
The Workers AI and AI Gateway team recently collaborated closely with security researchers at Ben Gurion University regarding a report submitted through our Public Bug Bounty program. Through this process, we discovered and fully patched a vulnerability affecting all LLM providers. Here’s the story
