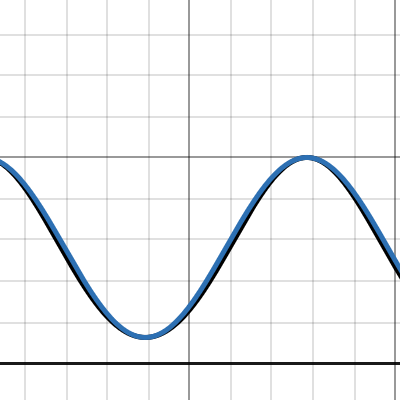
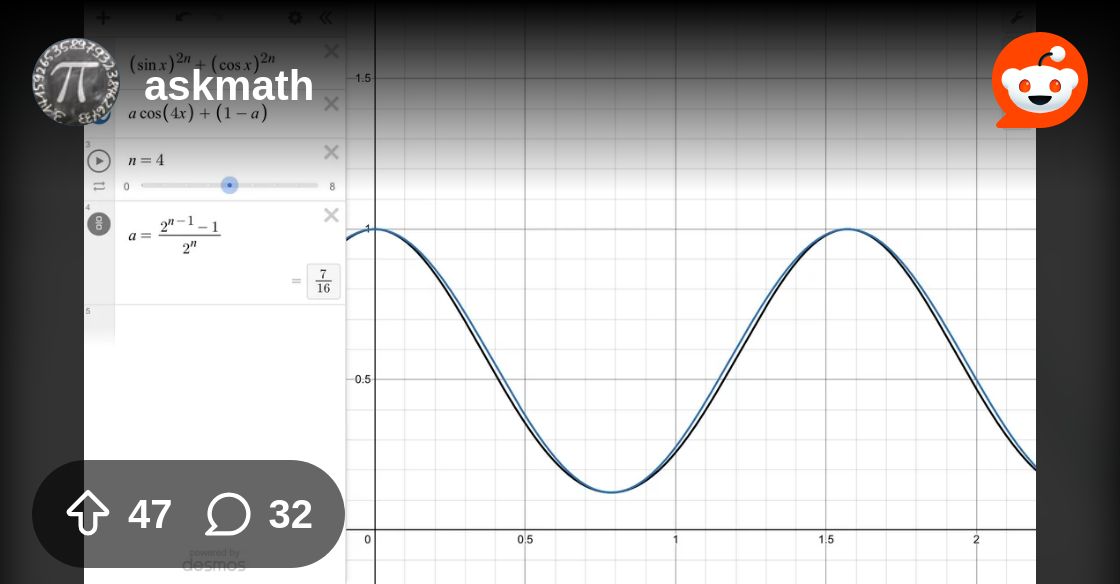
A “pattern” which breaks after n = 4. Any idea why?
I was experimenting with:
ƒ(x) = sin²ⁿ(x) + cos²ⁿ(x)
Where I found a pattern:
ƒ(x) = a⋅cos(4x) + (1-a) [a = (2ⁿ⁻¹-1)/2ⁿ]
The expression didn’t work at n = 0, but it seemed to hold for n = 1, 2, 3 and at n = 4 it finally broke. I don’t understand how from n = (1 to 3), ƒ(x) is a perfect sinusoidal wave but it fails to be one from after n = 4. Does anybody have any explanations as to why such pattern is followed and why does it break? (check out the attached desmos graph: https://www.desmos.com/calculator/p9boqzkvum )
As a side note, the expression: a⋅cos(4x) + (1-a), seems to be approaching: cos²(2x) as n→∞.
ƒ(x) = sin²ⁿ(x) + cos²ⁿ(x)
Where I found a pattern:
ƒ(x) = a⋅cos(4x) + (1-a) [a = (2ⁿ⁻¹-1)/2ⁿ]
The expression didn’t work at n = 0, but it seemed to hold for n = 1, 2, 3 and at n = 4 it finally broke. I don’t understand how from n = (1 to 3), ƒ(x) is a perfect sinusoidal wave but it fails to be one from after n = 4. Does anybody have any explanations as to why such pattern is followed and why does it break? (check out the attached desmos graph: https://www.desmos.com/calculator/p9boqzkvum )
As a side note, the expression: a⋅cos(4x) + (1-a), seems to be approaching: cos²(2x) as n→∞.