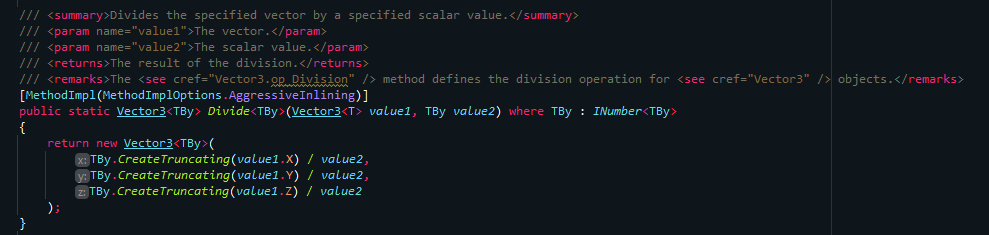
the problem here isn't how to do the computation
yes, it is very much intended to be done as floating-point and then cast to integer
(compute the infinitely precise result and round to the nearest representable result)
the problem comes in from how to implement that support generically and correctly
especially over time using where DIM implementations need to be provided
there also lies a slightly more general issue in that not everything can be represented equivalently
for example, Sqrt(-1.0f)Sqrt(-1.0f) produces NaNNaN, but it would have to throw for integer
likewise you end up not being able to represent infinites for trig functions
you end up with many other computations resulting in 0 or 1, regardless of input, due to it requiring fractional results
and so many operations functionally end up "pointless" for integrals